题目内容
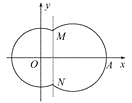
【题目】如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成,两相接点M,N均在直线x=5上.圆弧C1的圆心是坐标原点O,半径为13;圆弧C2过点A(29,0).
(1)求圆弧C2的方程.
(2)曲线C上是否存在点P,满足PA=![]() PO?若存在,指出有几个这样的点;若不存在,请说明理由.
PO?若存在,指出有几个这样的点;若不存在,请说明理由.
【答案】(1) (x-14)2+y2=225(5≤x≤29) (2) 不存在,理由见解析
【解析】
(1)圆弧C1所在圆的方程为x2+y2=169,令x=5,解得M(5,12),N(5, -12).
则线段AM中垂线的方程为y-6=2(x-17),令y=0,得圆弧C2所在圆的圆心为(14,0),
又圆弧C2所在圆的半径为r2=29-14=15,所以圆弧C2的方程为(x-14)2+y2=225(5≤x≤29).
(2)假设存在这样的点P(x,y),
则由PA=![]() PO,得x2+y2+2x-29=0,
PO,得x2+y2+2x-29=0,
由![]()
解得x=-70(舍去).
由![]()
解得x=0(舍去),
综上知,这样的点P不存在.
【误区警示】
求圆弧C2的方程时经常遗漏x的取值范围,其错误原因是将圆弧习惯认为或误认为圆.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目