ÌâÄżÄÚÈĘ
ĄŸÌâÄżĄż2019Äê4ÔÂŁŹŒŚÒÒÁœĐŁ”ÄѧÉúČÎŒÓÁËÄłżŒÊÔ»úččŸÙĐДĎóÁȘżŒŁŹÏÖŽÓŐâÁœĐŁČÎŒÓżŒÊÔ”ÄѧÉúÊęѧłÉŒšÔÚ100·ÖŒ°ÒÔÉÏ”ÄÊÔŸíÖĐÓĂÏ”ÍłłéŃù”Ä·œ·šžśłéÈĄÁË20·ĘÊÔŸíŁŹČąœ«Őâ40·ĘÊÔŸí”Ĕ÷ÖÖÆŚśłÉÈçÏ”ğ„Ҷ͌Łź
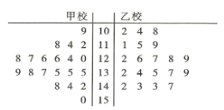
Łš1Ł©ÊÔÍščęŸ„Ò¶ÍŒ±ÈœÏŐâ40·ĘÊÔŸí”ÄÁœĐŁŃ§ÉúÊęѧłÉŒš”ÄÖĐλÊꣻ
Łš2Ł©Èô°ŃÊęѧłÉŒšČ»”ÍÓÚ135·Ö”ÄŒÇŚśÊęѧłÉŒšÓĆĐ㣏žùŸĘŸ„Ҷ͌ÖĐ”ÄÊęŸĘŁŹĆжÏÊÇ·ńÓĐ90![]() ”Ä°ŃÎŐÈÏÎȘÊęѧłÉŒšÔÚ100·ÖŒ°ÒÔÉÏ”ÄѧÉúÖĐÊęѧłÉŒšÊÇ·ńÓĆĐăÓëËùÔÚѧУÓĐčŰŁ»
”Ä°ŃÎŐÈÏÎȘÊęѧłÉŒšÔÚ100·ÖŒ°ÒÔÉÏ”ÄѧÉúÖĐÊęѧłÉŒšÊÇ·ńÓĆĐăÓëËùÔÚѧУÓĐčŰŁ»
Łš3Ł©ÈôŽÓŐâ40ĂûѧÉúÖĐŃĄÈĄÊęѧłÉŒšÔÚ![]() ”ÄѧÉúŁŹÓĂ·ÖČăłéŃù”Ä·œÊœŽÓŒŚÒÒÁœĐŁÖĐłéÈĄ5ÈËŁŹÔÙŽÓŐâ5ÈËÖĐËæ»úłéÈĄ3ÈË·ÖÎöÆäʧ·ÖÔÒòŁŹÇóŐâ3ÈËÖĐÇĄÓĐ2ÈËÊÇÒÒУѧÉú”ÄžĆÂÊŁź
”ÄѧÉúŁŹÓĂ·ÖČăłéŃù”Ä·œÊœŽÓŒŚÒÒÁœĐŁÖĐłéÈĄ5ÈËŁŹÔÙŽÓŐâ5ÈËÖĐËæ»úłéÈĄ3ÈË·ÖÎöÆäʧ·ÖÔÒòŁŹÇóŐâ3ÈËÖĐÇĄÓĐ2ÈËÊÇÒÒУѧÉú”ÄžĆÂÊŁź
ČÎżŒč«ÊœÓëÁÙœçÖ”±íŁș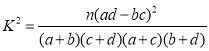 ŁŹÆäÖĐ
ŁŹÆäÖĐ![]() Łź
Łź
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
ĄŸŽđ°žĄż(1)ŒûœâÎöŁ»(2)ŒûœâÎöŁ»(3) ![]()
ĄŸœâÎöĄż
Łš1Ł©žùŸĘŸ„Ҷ͌·Ö±đÇółöŒŚÒÒÁœĐŁÊęѧłÉŒš”ÄÖĐλÊęșóœűĐĐ±ÈœÏŒŽżÉ”Ă”œœáÂÛŁźŁš2Ł©žùŸĘÌâÖĐÊęŸĘżÉ”ĂÁĐÁȘ±íŁŹÓɱíÖĐÊęŸĘ”Ă”œ![]() ŁŹÓÉŽËżÉ”ĂœáÂÛŁźŁš3Ł©žùŸĘ·ÖČăłéŃù”Ä·œ·šżÉ”ĂŽÓŒŚĐŁłéÈĄ2ÈËĄąÒÒĐŁłé3ÈËŁŹÈ»șóžùŸĘčĆ”äžĆĐÍžĆÂÊÇóœâŒŽżÉŁź
ŁŹÓÉŽËżÉ”ĂœáÂÛŁźŁš3Ł©žùŸĘ·ÖČăłéŃù”Ä·œ·šżÉ”ĂŽÓŒŚĐŁłéÈĄ2ÈËĄąÒÒĐŁłé3ÈËŁŹÈ»șóžùŸĘčĆ”äžĆĐÍžĆÂÊÇóœâŒŽżÉŁź
Łš1Ł©ÓÉŸ„Ҷ͌żÉÖȘŁŹŒŚĐŁŃ§ÉúÊęѧłÉŒš”ÄÖĐλÊęÎȘ![]() ŁŹÒÒУѧÉúÊęѧłÉŒš”ÄÖĐλÊęÎȘ
ŁŹÒÒУѧÉúÊęѧłÉŒš”ÄÖĐλÊęÎȘ![]() ŁŹ
ŁŹ
ËùÒÔŐâ40·ĘÊÔŸí”ÄłÉŒšŁŹŒŚĐŁŃ§ÉúÊęѧłÉŒš”ÄÖĐλÊę±ÈÒÒУѧÉúÊęѧłÉŒš”ÄÖĐλÊęžßŁź
Łš2Ł©ÓÉÌâÒ⣏”Ă”œ![]() ÁĐÁȘ±íÈçÏÂŁș
ÁĐÁȘ±íÈçÏÂŁș
ŒŚĐŁ | ÒÒĐŁ | șÏŒÆ | |
ÊęѧłÉŒšÓĆĐă | 10 | 7 | 17 |
ÊęѧłÉŒšČ»ÓĆĐă | 10 | 13 | 23 |
șÏŒÆ | 20 | 20 | 40 |
ÓɱíÖĐÊęŸĘżÉ”ĂŁŹ![]() ŁŹ
ŁŹ
ËùÒÔĂ»ÓĐ90![]() ”Ä°ŃÎŐÈÏÎȘÊęѧłÉŒšÔÚ100·ÖŒ°ÒÔÉÏ”ÄѧÉúÖĐÊęѧłÉŒšÊÇ·ńÓĆĐăÓëËùÔÚѧУÓĐčŰŁź
”Ä°ŃÎŐÈÏÎȘÊęѧłÉŒšÔÚ100·ÖŒ°ÒÔÉÏ”ÄѧÉúÖĐÊęѧłÉŒšÊÇ·ńÓĆĐăÓëËùÔÚѧУÓĐčŰŁź
Łš3Ł©Őâ40ĂûѧÉúÖĐÊęѧłÉŒšÔÚ![]() ”ÄŒŚĐŁÓĐ4ÈËŁŹÒÒĐŁÓĐ6ÈËŁŹÓĂ·ÖČăłéŃù”Ä·œÊœłéÈĄ5ÈËŁŹÔòŒŚĐŁłéÈĄ2ÈËŁŹ·Ö±đŒÇŚś
”ÄŒŚĐŁÓĐ4ÈËŁŹÒÒĐŁÓĐ6ÈËŁŹÓĂ·ÖČăłéŃù”Ä·œÊœłéÈĄ5ÈËŁŹÔòŒŚĐŁłéÈĄ2ÈËŁŹ·Ö±đŒÇŚś![]() Ł»ÒÒĐŁłé3ÈËŁŹ·Ö±đŒÇŚś
Ł»ÒÒĐŁłé3ÈËŁŹ·Ö±đŒÇŚś![]() Łź
Łź
ŽÓŐâ5ÈËÖĐËæ»úłéÈĄ3ÈËŁŹËùÓĐżÉÄܔĜáčûÓĐŁș![]()
![]() ŁŹčČ10ÖÖŁŹ
ŁŹčČ10ÖÖŁŹ
ÆäÖĐÒÒУѧÉúÇĄÓĐ2È˔ĜáčûÓĐŁș![]() ŁŹčČ6ÖÖŁŹ
ŁŹčČ6ÖÖŁŹ
ËùÒÔËùÇóžĆÂÊ![]() Łź
Łź

 ÓąČĆŒÆ»źÆÚÄ©”śŃĐÏ”ÁĐŽđ°ž
ÓąČĆŒÆ»źÆÚÄ©”śŃĐÏ”ÁĐŽđ°ž