题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,直线
时,直线![]() 与
与![]() 相切,求
相切,求![]() 的值;
的值;
(2)若函数![]() 在
在![]() 内有且只有一个零点,求此时函数
内有且只有一个零点,求此时函数![]() 的单调区间;
的单调区间;
(3)当![]() 时,若函数
时,若函数![]() 在
在![]() 上的最大值和最小值的和为1,求实数
上的最大值和最小值的和为1,求实数![]() 的值.
的值.
【答案】(1)![]() ; (2)单调递增区间为
; (2)单调递增区间为![]() ,
,![]() ,单调递减区间为
,单调递减区间为![]() ; (3)
; (3)![]() .
.
【解析】
(1)由![]() 求出切点坐标,代入切线方程即可得结果;(2)先证明当
求出切点坐标,代入切线方程即可得结果;(2)先证明当![]() 时不合题意,当
时不合题意,当![]() 时,根据单调性可得,要使函数
时,根据单调性可得,要使函数![]() 在
在![]() 内有且只有一个零点,则须
内有且只有一个零点,则须![]() ,求得
,求得![]() ,进而可得结果;(3)当
,进而可得结果;(3)当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,极大值为
上单调递减,极大值为![]() ,极小值为
,极小值为![]() ,且
,且![]() ,
,![]() ,分类讨论求出最大值与最小值,解方程即可得结果.
,分类讨论求出最大值与最小值,解方程即可得结果.
.
(1)![]() ,
,
则![]() ,所以,
,所以,![]() ,
,
当![]() ,所以
,所以![]() ,解得
,解得![]() .
.
(2)![]() ,
,
![]() 由
由![]() ,得到
,得到![]() ,
,![]() ,
,
当![]() 时,
时,![]() 在区间
在区间![]() 上恒成立,
上恒成立,
即函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
又因为函数![]() 的图象过点
的图象过点![]() ,即
,即![]() ,
,
所以函数![]() 在
在![]() 内没有零点,不合题意,
内没有零点,不合题意,
当![]() 时,由
时,由![]() 得
得![]() ,即函数
,即函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
由![]() 得
得![]() ,即函数
,即函数![]() 在区间在
在区间在![]() 上单调递减,
上单调递减,
且过点![]() ,要使函数
,要使函数![]() 在
在![]() 内有且只有一个零点,则须
内有且只有一个零点,则须![]() ,
,
即![]() ,解得
,解得![]() ,
,
综上可得函数![]() 在
在![]() 内有且只有一个零点时
内有且只有一个零点时![]() ,
,
此时函数![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() ,单调递减区间为
,单调递减区间为![]() .
.
(3)当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
此时函数![]() 有两个极值点,极大值为
有两个极值点,极大值为![]() ,极小值为
,极小值为![]() ,
,
且![]() ,
,![]() .
.
①当![]() 即
即![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,![]() ,
,
又![]() 即
即![]()
![]()
所以![]() ,解得
,解得![]() (舍).
(舍).
②当![]() 即
即![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
在![]() 上单调递增
上单调递增 ![]() 即
即![]() ,所以
,所以![]() .
.
若![]() ,即
,即![]() 时,
时,![]() ,所以
,所以![]() ,
,
解得![]() (舍).
(舍).
若![]() ,即
,即![]() 时,
时,![]() ,所以
,所以![]() ,
,
解得![]() .
.
综上,![]() .
.

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案【题目】为建立健全国家学生体质健康监测评价机制,激励学生积极参加身体锻炼,教育部印发《国家学生体质健康标准(2014年修订)》,要求各学校每学期开展覆盖本校各年级学生的《标准》测试工作,并根据学生每个学期总分评定等级.某校决定针对高中学生,每学期进行一次体质健康测试,以下是小明同学六个学期体质健康测试的总分情况.
学期 | 1 | 2 | 3 | 4 | 5 | 6 |
总分 | 512 | 518 | 523 | 528 | 534 | 535 |
(1)请根据上表提供的数据,用相关系数![]() 说明
说明![]() 与
与![]() 的线性相关程度,并用最小二乘法求出
的线性相关程度,并用最小二乘法求出![]() 关于
关于![]() 的线性回归方程(线性相关系数保留两位小数);
的线性回归方程(线性相关系数保留两位小数);
(2)在第六个学期测试中学校根据 《标准》,划定540分以上为优秀等级,已知小明所在的学习小组10个同学有6个被评定为优秀,测试后同学们都知道了自己的总分但不知道别人的总分,小明随机的给小组内4个同学打电话询问对方成绩,优秀的同学有![]() 人,求
人,求![]() 的分布列和期望.
的分布列和期望.
参考公式: 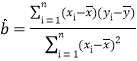 ,
,![]() ;
;
相关系数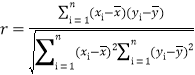 ;
;
参考数据:![]() ,
,![]() .
.
【题目】某校进行课题实验,乙班为实验班,甲班为对比班,甲乙两班均有50人,一年后对两班进行测试,成绩如下表
甲班成绩 |
|
|
|
|
|
人数 | 4 | 20 | 15 | 10 | 1 |
乙班成绩 |
|
|
|
|
|
人数 | 1 | 11 | 23 | 13 | 2 |
(1)现从甲班成绩位于![]() 内的试卷中抽取9份进行试卷分析,请问用什么抽样方法更合理,并写出最后的抽样结果
内的试卷中抽取9份进行试卷分析,请问用什么抽样方法更合理,并写出最后的抽样结果
(2)完成下列![]() 列联表,并判断有多大把握认为这两个班在这次测试中成绩的差异与实施课题实验有关。
列联表,并判断有多大把握认为这两个班在这次测试中成绩的差异与实施课题实验有关。
成绩小于100 | 成绩不小于100 | 合计 | |
甲班 | 50 | ||
乙班 | 50 | ||
合计 | 36 | 64 | 100 |