题目内容
20.设圆C的极坐标方程为ρ=2,以极点为直角坐标系的原点,极轴为x轴正半轴,两坐标系长度单位一致,建立平面直角坐标系.过圆C上的一点M(m,s)作垂直于x轴的直线l:x=m,设l与x轴交于点N,向量$\overrightarrow{OQ}=\overrightarrow{OM}+\overrightarrow{ON}$.(Ⅰ)求动点Q的轨迹方程;
(Ⅱ)设点R(1,0),求$|{\overrightarrow{RQ}}|$的最小值.
分析 (Ⅰ)由已知得N是坐标(m,0),设出Q(x,y),由$\overrightarrow{OQ}=\overrightarrow{OM}+\overrightarrow{ON}$,得到M的坐标与Q坐标的关系,然后利用M在ρ=2上求得动点Q的轨迹方程;
(Ⅱ)写出Q的参数方程,利用两点间的距离公式得到$|{\overrightarrow{RQ}}|$,然后利用配方法求最值.
解答 解:(Ⅰ)由已知得N是坐标(m,0),
设Q(x,y),由$\overrightarrow{OQ}=\overrightarrow{OM}+\overrightarrow{ON}$,得
$\left\{\begin{array}{l}{x=2m}\\{y=s}\end{array}\right.$,则$\left\{\begin{array}{l}{m=\frac{x}{2}}\\{s=y}\end{array}\right.$,
∵点M在圆ρ=2上,即在m2+s2=4上,
∴$\frac{x^2}{4}+{y^2}=4$,
∴Q是轨迹方程为 $\frac{x^2}{16}+\frac{y^2}{4}=1$;
(Ⅱ)Q点的参数方程为$\left\{\begin{array}{l}x=4cosθ\\ y=2sinθ\end{array}\right.$,
∴$|{\overrightarrow{RQ}}|=\sqrt{{{(4cosθ-1)}^2}+4{{sin}^2}θ}=\sqrt{12{{cos}^2}θ-8cosθ+5}=\sqrt{12{{(cosθ-\frac{1}{3})}^2}+\frac{11}{3}}$
$≥\sqrt{\frac{11}{3}}=\frac{{\sqrt{33}}}{3}$.
则$|{\overrightarrow{RQ}}|$的最小值为$\frac{{\sqrt{33}}}{3}$.
点评 本题考查简单曲线的极坐标方程,训练了利用代入法求动点的轨迹方程,训练了利用配方法求最值,是中档题.

| A. | $\frac{3}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
| x | 2 | 5 | 3 | 1 | 4 |
| f(x) | 1 | 2 | 3 | 4 | 5 |
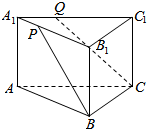 如图,在三棱柱ABC-A1B1C1中,B1P=2PA1,C1Q=2QA1,求证:直线AA1,BP,CQ相交于一点.
如图,在三棱柱ABC-A1B1C1中,B1P=2PA1,C1Q=2QA1,求证:直线AA1,BP,CQ相交于一点.