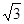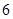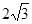题目内容
在△ABC中,满足
与
的夹角为60°,M是AB的中点,
(1)若|
|=|
|,求向量
+2
与
的夹角的余弦值;.
(2)若|
|=2,|
|=2
,点D在边AC上,且
=λ
,如果
•
=0,求λ的值.
| AB |
| AC |
(1)若|
| AB |
| AC |
| AB |
| AC |
| AB |
(2)若|
| AB |
| BC |
| 3 |
| AD |
| AC |
| MD |
| AC |
(1)设|
|=1,
•
=|
|•|
|cos60°=
,
则|
+2
|=
=
=
而
•(
+2
)=2,
所以向量
+2
与
的夹角的余弦值等于cosθ=
=
=
.
(2)在|
|2=|
|2+|
|2-2|
|•|
|•cos60°,
解得|
|=4,
因为
⊥
,所以|
|=cos60°=
,
故λ=
.
| AB |
| AB |
| AC |
| AB |
| AC |
| 1 |
| 2 |
则|
| AB |
| AC |
|
|
1+4×
|
| 7 |
而
| AB |
| AB |
| AC |
所以向量
| AB |
| AC |
| AB |
| ||||||
|
|
| 2 | ||
|
2
| ||
| 7 |
(2)在|
| BC |
| AC |
| AB |
| AB |
| AC |
解得|
| AC |
因为
| MD |
| AC |
| AD |
| 1 |
| 2 |
故λ=
| 1 |
| 8 |

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
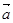 与
与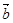 的夹角为
的夹角为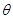 ,定义
,定义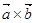 为
为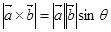 ,若
,若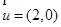 ,
,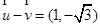 ,则
,则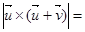 ( )
( )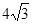 B.
B.