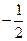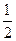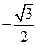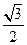题目内容
已知定点F(1,0),动点P(异于原点)在y轴上运动,连接FP,过点P作PM交x轴于点M,并延长MP到点N,且
•
=0,|
|=|
|.
(1)求动点N的轨迹C的方程;
(2)若直线l与动点N的轨迹交于A、B两点,若
•
=-4且4
≤|AB|≤4
,求直线l的斜率k的取值范围.
| PM |
| PF |
| PN |
| PM |
(1)求动点N的轨迹C的方程;
(2)若直线l与动点N的轨迹交于A、B两点,若
| OA |
| OB |
| 6 |
| 30 |
(1)设动点N(x,y),则M(-x,0),P(0,
)(x>0),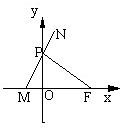
∵PM⊥PF,∴kPMkPF=-1,即
•
=-1,
∴y2=4x(x>0)即为所求.
(2)设直线l方程为y=kx+b,l与抛物线交于点A(x1,y1)、B(x2,y2),
则由
•
=-4,得x1x2+y1y2=-4,即
+y1y2=-4,∴y1y2=-8,
由
可得ky2-4y+4b=0(其中k≠0),∴y1y2=
=-8,b=-2k,
当△=16-16kb=16(1+2k2)>0时,|AB|2=(1+
)(y2-y1)2=
•[(y2+y1)2-4y1•y2]=
(
+32).
由题意,得16×6≤
•≤16×30,解得
≤k2≤1,
∴
≤k≤1,或-1≤k≤-
.
即所求k的取值范围是[-1,-
]∪[
1].
| y |
| 2 |

∵PM⊥PF,∴kPMkPF=-1,即
| ||
| x |
| ||
| -1 |
∴y2=4x(x>0)即为所求.
(2)设直线l方程为y=kx+b,l与抛物线交于点A(x1,y1)、B(x2,y2),
则由
| OA |
| OB |
| y12•y22 |
| 16 |
由
|
| 4b |
| k |
当△=16-16kb=16(1+2k2)>0时,|AB|2=(1+
| 1 |
| k2 |
| 1+k2 |
| k2 |
| 1+k2 |
| k2 |
| 16 |
| k2 |
由题意,得16×6≤
| 1+k2 |
| k2 |
| 1 |
| 4 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
即所求k的取值范围是[-1,-
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
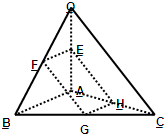
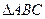 中,设
中,设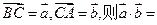 ( )
( )