题目内容
10.由数字1,3,4,6,x五个数字组成没有重复数字的五位数,所有这些五位数各位上的数字之和的总值为2640,则x=8.分析 根据题意,按x是否为0分2种情况讨论:(1)x=0(2)x≠0,每种情况下先求出5个数字可以组成五位数的个数,进而表示出这些五位数各位上的数字之和,求出x的值,即可得答案.
解答 解:根据题意,分2种情况讨论:
(1)若x=0,这5个数字为1、3、4、6、0,可以组成4A44=96个没有重复数字的五位数,
则1、3、4、6、0中每个数字均出现96次,
所有这些五位数各位上的数字之和为96×(1+3+4+6)=1344≠2640,
故x=0不符合题意;
(2)若x≠0,这5个数字可以组成A55=120个没有重复数字的五位数,
则1、3、4、6、x中每个数字均出现120次,
又由所有这些五位数各位上的数字之和为2640,
则有120×(1+3+4+6+x)=2640,
解可得x=8;
综合可得x=8;
故答案为:8.
点评 本题考查排列、组合的应用,注意解题时要分x是否为0进行讨论,其次注意“所有这些五位数各位上的数字之和”的含义.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案
相关题目
18.某高中的4名高三学生计划在高考结束后到西藏、新疆、香港等3个地区去旅游,要求每个地区都要有学生去,每个学生只去一个地区旅游,且学生甲不到香港,则不同的出行安排有( )
| A. | 36种 | B. | 28种 | C. | 24种 | D. | 22种 |
2. 在某海滨小城打的士收费办法如下:不超过3公里收8元,超过3公里的里程每公里收2.6元,另每车次超过3公里收燃油附加费1元(其他因素不考虑).相应x>3收费系统的流程图如图所示,则①处应填( )
在某海滨小城打的士收费办法如下:不超过3公里收8元,超过3公里的里程每公里收2.6元,另每车次超过3公里收燃油附加费1元(其他因素不考虑).相应x>3收费系统的流程图如图所示,则①处应填( )
 在某海滨小城打的士收费办法如下:不超过3公里收8元,超过3公里的里程每公里收2.6元,另每车次超过3公里收燃油附加费1元(其他因素不考虑).相应x>3收费系统的流程图如图所示,则①处应填( )
在某海滨小城打的士收费办法如下:不超过3公里收8元,超过3公里的里程每公里收2.6元,另每车次超过3公里收燃油附加费1元(其他因素不考虑).相应x>3收费系统的流程图如图所示,则①处应填( )| A. | y=8+2.6x | B. | y=9+2.6x | C. | y=8+2.6(x-3) | D. | y=9+2.6(x-3) |
20. 某种产品的广告费用支出x万元与销售额y万元之间有如下的对应数据:
某种产品的广告费用支出x万元与销售额y万元之间有如下的对应数据:
(1)画出散点图;
(2)求回归直线方程;
(3)据此估计广告费用为12万元时,销售收入y的值.
附:线性回归方程:$\stackrel{∧}{y}$=bx+a,其中b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$=$\frac{\overline{xy}-\overline{x}\overline{y}}{\overline{{x}^{2}}-{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$.
 某种产品的广告费用支出x万元与销售额y万元之间有如下的对应数据:
某种产品的广告费用支出x万元与销售额y万元之间有如下的对应数据:| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
(2)求回归直线方程;
(3)据此估计广告费用为12万元时,销售收入y的值.
附:线性回归方程:$\stackrel{∧}{y}$=bx+a,其中b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$=$\frac{\overline{xy}-\overline{x}\overline{y}}{\overline{{x}^{2}}-{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$.
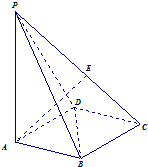 如图,底面为菱形的四棱锥P-ABCD中,PA⊥面ABCD,∠ABD=60°,E为PC上一动点,PA=AC.
如图,底面为菱形的四棱锥P-ABCD中,PA⊥面ABCD,∠ABD=60°,E为PC上一动点,PA=AC.