题目内容
14.假设在6分钟内的任意时刻,两架相同型号的飞机机会均等地进入同一飞机场,若这两架飞机进入机场的时间之差不小于2分钟,飞机不会受到干扰;则飞机受到干扰的概率为$\frac{5}{9}$.分析 分别设两个互相独立的飞机为x,y,根据题意表示出x与y的范围,由这两架飞机进入机场的时间之差不小于2分钟,飞机不会受到干扰,列出飞机受到干扰的事件发生x与y的关系式,找出约束条件$\left\{\begin{array}{l}{0≤x≤6}\\{0≤y≤6}\\{|x-y|≤2}\end{array}\right.$ 的可行域为如图阴影部分,阴影区域面积和正方形面积比值即为干扰发生的概率.
解答 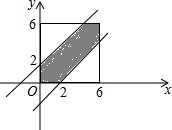 解:分别设两个互相独立的飞机为x,y,
解:分别设两个互相独立的飞机为x,y,
则所有事件集可表示为0≤x≤6,0≤y≤6,
由题目得,如果飞机受到干扰的事件发生,必有|x-y|≤2,
此时x,y满足$\left\{\begin{array}{l}{0≤x≤6}\\{0≤y≤6}\\{|x-y|≤2}\end{array}\right.$,约束条件$\left\{\begin{array}{l}{0≤x≤6}\\{0≤y≤6}\\{|x-y|≤2}\end{array}\right.$ 的可行域为如图阴影部分,
而所有事件的集合即为正方型面积,阴影区域面积为62-2×$\frac{1}{2}$×(6-2)2=36-16=20,
则阴影区域面积和正方形面积比值即为干扰发生的概率,即P=$\frac{20}{36}$=$\frac{5}{9}$,
故答案为:$\frac{5}{9}$.
点评 此题考查了几何概型,确定出约束条件的可行域是解本题的关键.

练习册系列答案
相关题目
4.“孝敬父母.感恩社会”是中华民族的传统美德.从出生开始,父母就对们关心无微不至,其中对我们物质帮助是最重要的一个指标,下表是一个统计员在统计《父母为我花了多少》当中使用处理得到下列的数据:
参考数据公式:$\sum_{i=1}^6{x_i}{y_i}$=1024.6,$\sum_{i=1}^6{{x_i}^2}$=730,
线性回归方程:$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,($\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{n=i}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$$\overline{x}$)
假设花费累积y与岁数x符合线性相关关系,求
(1)花费累积y与岁数x的线性回归直线方程(系数保留3位小数);
(2)24岁大学毕业之后,我们不再花父母的钱,假设你在30岁成家立业之后,在你50岁之前偿还父母为你的花费(不计利息).那么你每月要偿还父母约多少元钱?
参考数据公式:$\sum_{i=1}^6{x_i}{y_i}$=1024.6,$\sum_{i=1}^6{{x_i}^2}$=730,
线性回归方程:$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,($\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{n=i}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$$\overline{x}$)
| 岁数x | 1 | 2 | 6 | 12 | 16 | 17 |
| 花费累积y(万元) | 1 | 2.8 | 9 | 17 | 22 | 24 |
(1)花费累积y与岁数x的线性回归直线方程(系数保留3位小数);
(2)24岁大学毕业之后,我们不再花父母的钱,假设你在30岁成家立业之后,在你50岁之前偿还父母为你的花费(不计利息).那么你每月要偿还父母约多少元钱?
2. 在某海滨小城打的士收费办法如下:不超过3公里收8元,超过3公里的里程每公里收2.6元,另每车次超过3公里收燃油附加费1元(其他因素不考虑).相应x>3收费系统的流程图如图所示,则①处应填( )
在某海滨小城打的士收费办法如下:不超过3公里收8元,超过3公里的里程每公里收2.6元,另每车次超过3公里收燃油附加费1元(其他因素不考虑).相应x>3收费系统的流程图如图所示,则①处应填( )
 在某海滨小城打的士收费办法如下:不超过3公里收8元,超过3公里的里程每公里收2.6元,另每车次超过3公里收燃油附加费1元(其他因素不考虑).相应x>3收费系统的流程图如图所示,则①处应填( )
在某海滨小城打的士收费办法如下:不超过3公里收8元,超过3公里的里程每公里收2.6元,另每车次超过3公里收燃油附加费1元(其他因素不考虑).相应x>3收费系统的流程图如图所示,则①处应填( )| A. | y=8+2.6x | B. | y=9+2.6x | C. | y=8+2.6(x-3) | D. | y=9+2.6(x-3) |
6.某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在1~50名和951~1000名的学生进行了调查,得到如下数据:
(1)根据表中的数据,能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系?
(2)根据表中数据,在调查的100名学生中,按照分层抽样在不近视的学生中抽取了9人,进一步调查他们良好的护眼习惯,并且在这9人中任取3人,记名次在1~50名的学生人数为X,求X的分布列和数学期望.
附:P(K2≥3.841=0.05)K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
(1)根据表中的数据,能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系?
(2)根据表中数据,在调查的100名学生中,按照分层抽样在不近视的学生中抽取了9人,进一步调查他们良好的护眼习惯,并且在这9人中任取3人,记名次在1~50名的学生人数为X,求X的分布列和数学期望.
| 年级名次 是否近视 | 1~50 | 951~1000 |
| 近视 | 41 | 32 |
| 不近视 | 9 | 18 |
4.为了考察高中生的性别与是否喜欢数学课程之间的关系,在某城市的某校的高中生中随机地抽取了300名学生进行调查,得到如下列联表:
由表中数据计算K2≈4.513,判断高中生的性别与是否喜欢数学课程之间是否有关系,并说明理由.
| 喜欢数学 | 不喜欢数学 | 总计 | |
| 男 | 37 | 85 | 122 |
| 女 | 35 | 143 | 178 |
| 总计 | 72 | 228 | 300 |
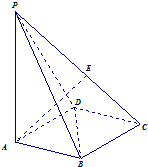 如图,底面为菱形的四棱锥P-ABCD中,PA⊥面ABCD,∠ABD=60°,E为PC上一动点,PA=AC.
如图,底面为菱形的四棱锥P-ABCD中,PA⊥面ABCD,∠ABD=60°,E为PC上一动点,PA=AC.