题目内容
15.已知直线l:y=k(x+2$\sqrt{2}$)(k≠0)与圆O:x2+y2=4相交于A,B两点,O为坐标原点,△AOB的面积为S.(1)当k=$\frac{\sqrt{2}}{2}$时,求S的值;
(2)求S的最大值,并求出此时的k值.
分析 (1)作OD⊥AB于D,当k=$\frac{\sqrt{2}}{2}$时,直线l:y=$\frac{\sqrt{2}}{2}$x+2,求出|AB|,|OD|,即可求出S的值;
(2)设∠AOB=θ(0θ<180°),则S=$\frac{1}{2}$|OA||OB|sinθ=2sinθ,即可求S的最大值,从而求出此时的k值.
解答 解:(1)作OD⊥AB于D,当k=$\frac{\sqrt{2}}{2}$时,直线l:y=$\frac{\sqrt{2}}{2}$x+2,则|OD|=$\frac{2}{\sqrt{1+\frac{1}{2}}}$=$\frac{2\sqrt{6}}{3}$,…(2分)
|AB|=2$\sqrt{4-\frac{8}{3}}$=$\frac{4\sqrt{3}}{3}$,…(4分)
∴S=$\frac{1}{2}$|AB||OD|=$\frac{4\sqrt{2}}{3}$;…(6分)
(2)设∠AOB=θ(0θ<180°)
则S=$\frac{1}{2}$|OA||OB|sinθ=2sinθ,…(8分)
∴当θ=90°时,S(θ)max=2,此时|OD|=$\sqrt{2}$,…(10分)
即$\frac{2\sqrt{2}|k|}{\sqrt{1+{k}^{2}}}$=$\sqrt{2}$,
∴k=±$\frac{\sqrt{3}}{3}$.…(12分)
点评 本题考查直线与圆的位置关系,点到直线的距离,三角形面积公式的应用,考查计算能力.

练习册系列答案
相关题目
6.某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在1~50名和951~1000名的学生进行了调查,得到如下数据:
(1)根据表中的数据,能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系?
(2)根据表中数据,在调查的100名学生中,按照分层抽样在不近视的学生中抽取了9人,进一步调查他们良好的护眼习惯,并且在这9人中任取3人,记名次在1~50名的学生人数为X,求X的分布列和数学期望.
附:P(K2≥3.841=0.05)K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
(1)根据表中的数据,能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系?
(2)根据表中数据,在调查的100名学生中,按照分层抽样在不近视的学生中抽取了9人,进一步调查他们良好的护眼习惯,并且在这9人中任取3人,记名次在1~50名的学生人数为X,求X的分布列和数学期望.
| 年级名次 是否近视 | 1~50 | 951~1000 |
| 近视 | 41 | 32 |
| 不近视 | 9 | 18 |
20. 某种产品的广告费用支出x万元与销售额y万元之间有如下的对应数据:
某种产品的广告费用支出x万元与销售额y万元之间有如下的对应数据:
(1)画出散点图;
(2)求回归直线方程;
(3)据此估计广告费用为12万元时,销售收入y的值.
附:线性回归方程:$\stackrel{∧}{y}$=bx+a,其中b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$=$\frac{\overline{xy}-\overline{x}\overline{y}}{\overline{{x}^{2}}-{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$.
 某种产品的广告费用支出x万元与销售额y万元之间有如下的对应数据:
某种产品的广告费用支出x万元与销售额y万元之间有如下的对应数据:| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
(2)求回归直线方程;
(3)据此估计广告费用为12万元时,销售收入y的值.
附:线性回归方程:$\stackrel{∧}{y}$=bx+a,其中b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$=$\frac{\overline{xy}-\overline{x}\overline{y}}{\overline{{x}^{2}}-{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$.
7.已知$sin(α+\frac{π}{3})+sinα$=-$\frac{{4\sqrt{3}}}{5},-\frac{π}{2}$<α<0,则cosα=( )
| A. | $\frac{{3\sqrt{3}+4}}{10}$ | B. | $\frac{{3\sqrt{3}-4}}{10}$ | C. | $\frac{{4-3\sqrt{3}}}{10}$ | D. | $-\frac{{3\sqrt{3}+4}}{10}$ |
4.为了考察高中生的性别与是否喜欢数学课程之间的关系,在某城市的某校的高中生中随机地抽取了300名学生进行调查,得到如下列联表:
由表中数据计算K2≈4.513,判断高中生的性别与是否喜欢数学课程之间是否有关系,并说明理由.
| 喜欢数学 | 不喜欢数学 | 总计 | |
| 男 | 37 | 85 | 122 |
| 女 | 35 | 143 | 178 |
| 总计 | 72 | 228 | 300 |
14.定积分:$\int_{-\frac{π}{2}}^{\frac{π}{2}}{({x+sinx})}dx$=( )
| A. | $\frac{π^2}{8}+1$ | B. | $\frac{π^2}{4}+2$ | C. | 1 | D. | 0 |
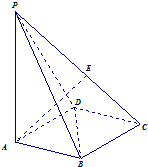 如图,底面为菱形的四棱锥P-ABCD中,PA⊥面ABCD,∠ABD=60°,E为PC上一动点,PA=AC.
如图,底面为菱形的四棱锥P-ABCD中,PA⊥面ABCD,∠ABD=60°,E为PC上一动点,PA=AC. 如图,已知A(x1,y1)为抛物线y2=2px(p>0)上的动点,P(p,0)为定点.
如图,已知A(x1,y1)为抛物线y2=2px(p>0)上的动点,P(p,0)为定点.