题目内容
17.已知直线l过点M(1,1),且与x轴、y轴的正半轴分别交与点A,B,则当|MA|2+|MB|2取得最小值时,直线l的方程为x+y-2=0.分析 设直线方程为y-1=k(x-1)(k>0),则A(-$\frac{1}{k}$+1,0),B(0,1-k),可得|MA|2+|MB|2=(-$\frac{1}{k}$)2+1+1+(-k)2=2+k2+$\frac{1}{{k}^{2}}$,利用基本不等式,即可得出结论.
解答 解:设直线方程为y-1=k(x-1)(k>0),则A(-$\frac{1}{k}$+1,0),B(0,1-k),
∴|MA|2+|MB|2=(-$\frac{1}{k}$)2+1+1+(-k)2=2+k2+$\frac{1}{{k}^{2}}$≥2+2=4,
当且仅当k2=1时取等号,此时k=-1,
∴当|MA|2+|MB|2取得最小值时,直线l的方程为y-1=-x+1,即x+y-2=0,
故答案为:x+y-2=0.
点评 本题考查直线方程,考查两点间距离公式的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
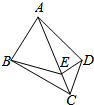 如图,空间四边形ABCD,∠CAD=45°,cos∠ACB=$\frac{\sqrt{15}}{5}$,AC=$\sqrt{15}$+$\sqrt{10}$,AD=2$\sqrt{5}$,BC=6,若点E在线段AC上运动,则EB+ED的最小值为7.
如图,空间四边形ABCD,∠CAD=45°,cos∠ACB=$\frac{\sqrt{15}}{5}$,AC=$\sqrt{15}$+$\sqrt{10}$,AD=2$\sqrt{5}$,BC=6,若点E在线段AC上运动,则EB+ED的最小值为7.