题目内容
13.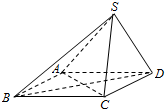 已知在四棱锥S-ABCD中,底面ABCD是平行四边形,若SB⊥AC,SA=SC.
已知在四棱锥S-ABCD中,底面ABCD是平行四边形,若SB⊥AC,SA=SC.(1)求证:平面SBD⊥平面ABCD;
(2)若AB=2,SB=3,cos∠SCB=-$\frac{1}{8}$,∠SAC=60°,求四棱锥S-ABCD的体积.
分析 (1)证明AC⊥平面SBD,即可证明平面SBD⊥平面ABCD;
(2)确定底面ABCD是菱形,求出SC,SO,BO,即可求四棱锥S-ABCD的体积.
解答  (1)证明:设AC∩BD=O,连接SO,则
(1)证明:设AC∩BD=O,连接SO,则
∵SA=SC,∴AC⊥SO,
∵SB⊥AC,SO∩SB=S,
∴AC⊥平面SBD,
∵AC?平面ABCD,
∴平面SBD⊥平面ABCD;
(2)解:由(1)知,SO⊥平面ABCD,AC⊥BD,∴底面ABCD是菱形,
∴BC=AB=2,
∵SB=3,cos∠SCB=-$\frac{1}{8}$,
∴由余弦定理可得SC=2,
∵∠SAC=60°,
∴△SAC是等边三角形,
∴SO=$\sqrt{3}$,
∴BO=$\sqrt{6}$,
∴VS-ABCD=$\frac{1}{3}×\frac{1}{2}×2×2\sqrt{6}×\sqrt{3}$=2$\sqrt{2}$.
点评 本题考查求四棱锥S-ABCD的体积,考查线面、面面垂直,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
2.F为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1的右焦点,点P在双曲线右支上,△POF(O为坐标原点)是面积为$\sqrt{3}$的等边三角形,则双曲线的离心率为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\sqrt{3}$+1 |
2.设函数f1(x)=x2,f2(x)=2(x-x2),ai=$\frac{i}{99}$,i=0,1,2,…,99,记Sk=|fk(a1)-fk(a0)|+|fk(a2)-fk(a1)|+…+|fk(a99)-fk(a98)|,k=1,2,则下列结论正确的是( )
| A. | S1=1<S2 | B. | S1=1>S2 | C. | S1>1>S2 | D. | S1<1<S2 |
 如图,F是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左焦点,椭圆的离心率为$\frac{1}{2}$.A,B为椭圆的左顶点和上顶点,点C在x轴上,BC⊥BF,△BCF的外接圆M恰好与直线l1:x+$\sqrt{3}$y+3=0相切.
如图,F是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左焦点,椭圆的离心率为$\frac{1}{2}$.A,B为椭圆的左顶点和上顶点,点C在x轴上,BC⊥BF,△BCF的外接圆M恰好与直线l1:x+$\sqrt{3}$y+3=0相切.