题目内容
14.我们规定:对于任意实数A,若存在数列{an}和实数x(x≠0),使得A=a1+a2x+a3x2+…+anxn-1,则称数A可以表示成x进制形式,简记为:A=$\overline{x({a}_{1})({a}_{2})({a}_{3})…({a}_{n-1})({a}_{n})}$.如:A=$\overline{2(-1)(3)(-2)(1)}$,则表示A是一个2进制形式的数,且A=-1+3×2+(-2)×22+1×23=5.(1)已知m=(1-2x)(1+3x2)(其中x≠0),试将m表示成x进制的简记形式.
(2)若数列{an}满足a1=2,ak+1=$\frac{1}{{1-{a_k}}},k∈{N^*}$,bn=$\overline{2({a}_{1})({a}_{2})({a}_{3})…({a}_{3n-2})({a}_{3n-1})({a}_{3n})}$(n∈N*),是否存在实常数p和q,对于任意的n∈N*,bn=p•8n+q总成立?若存在,求出p和q;若不存在,说明理由.
(3)若常数t满足t≠0且t>-1,dn=$\overline{2({C}_{n}^{1})({C}_{n}^{2})({C}_{n}^{3})…({C}_{n}^{n-1})({C}_{n}^{n})}$,求$\lim_{n→∞}\frac{d_n}{{{d_{n+1}}}}$.
分析 (1)化简m,由新定义即可得到所求;
(2)分别求得数列的前几项,可得数列是周期为3的数列,假设存在实常数p和q,对于任意的n∈N*,${b_n}=p•{8^n}+q$总成立,化简整理,运用等比数列的求和公式,计算即可得到;
(3)由新定义化简整理,运用二项式定理,结合数列极限的求法,即可得到.
解答 解:(1)m=(1-2x)(1+3x2)=1-2x+3x2-6x3
则m=$\overline{x(1)(-2)(3)(-6)}$;
(2)${a_2}=-1,{a_3}=\frac{1}{2},{a_4}=2,{a_5}=-1,{a_6}=\frac{1}{2}$,
∵${a_{n+1}}=\frac{1}{{1-{a_n}}}$∴${a_{n+2}}=\frac{1}{{1-{a_{n+1}}}}=\frac{1}{{1-\frac{1}{{1-{a_n}}}}}=\frac{{1-{a_n}}}{{-{a_n}}}$
∴${a_{n+3}}=\frac{1}{{1-{a_{n+2}}}}=\frac{1}{{1+\frac{{1-{a_n}}}{a_n}}}$=an(n∈N*),
则{an}是周期为3的数列,
假设存在实常数p和q,对于任意的n∈N*,${b_n}=p•{8^n}+q$总成立,
则bn=$\overline{2({a}_{1})({a}_{2})({a}_{3})…({a}_{3n-2})({a}_{3n-1})({a}_{3n})}$
=$[2+(-1)×2+\frac{1}{2}×{2^2}]+[2×{2^3}+(-1)×{2^4}+\frac{1}{2}×{2^5}]$$+…+[2×{2^{3n-3}}+(-1)×{2^{3n-2}}+\frac{1}{2}×{2^{3n-1}}]$
=$[2+(-1)×2+\frac{1}{2}×{2^2}]×(1+{2^3}+{2^6}+…+{2^{3n-3}})$=$2×\frac{{1-{8^n}}}{1-8}=\frac{2}{7}×{8^n}-\frac{2}{7}$,
∴$p=\frac{2}{7},q=-\frac{2}{7}$.
即存在实常数$p=\frac{2}{7},q=-\frac{2}{7}$,对于任意的n∈N*,${b_n}=\frac{2}{7}•{8^n}-\frac{2}{7}$总成立;
(3)dn=$\overline{2({C}_{n}^{1})({C}_{n}^{2})({C}_{n}^{3})…({C}_{n}^{n-1})({C}_{n}^{n})}$=${C}_{n}^{1}$+2${C}_{n}^{2}$+4${C}_{n}^{3}$+…+2n-1${C}_{n}^{n}$
=$\frac{{2C}_{n}^{1}+{4C}_{n}^{2}+…+{{2}^{n}C}_{n}^{n}}{2}$=$\frac{{C}_{n}^{0}{+2C}_{n}^{1}+…+{{2}^{n}C}_{n}^{n}-1}{2}$=$\frac{1}{2}$(3n-1),
∴$\lim_{n→∞}\frac{d_n}{{{d_{n+1}}}}$=$\underset{lim}{n→∞}$$\frac{{3}^{n}-1}{{3}^{n+1}-1}$=$\frac{1}{3}$.
点评 本题考查新定义的理解和运用,同时考查数列的周期性和二项式定理的运用,以及数列极限的求法,考查运算能力,具有一定的综合性.

 名校课堂系列答案
名校课堂系列答案| A. | S1=1<S2 | B. | S1=1>S2 | C. | S1>1>S2 | D. | S1<1<S2 |
| A. | l1∥l2 | B. | l1⊥l2 | C. | l1和l2重合 | D. | l1,l2斜交 |
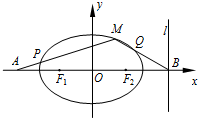 在平面直角坐标系xOy中,设中心在坐标原点的椭圆C的左、右焦点分别为F1、F2,右准线l:x=m+1与x轴的交点为B,BF2=m.
在平面直角坐标系xOy中,设中心在坐标原点的椭圆C的左、右焦点分别为F1、F2,右准线l:x=m+1与x轴的交点为B,BF2=m.