题目内容
14.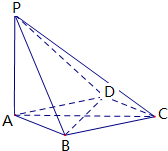 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是边长为1的菱形,且∠BAD=60°,
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是边长为1的菱形,且∠BAD=60°,(Ⅰ)求证:平面PBD⊥平面PAC;
(Ⅱ)若PA=$\sqrt{3}$,求三棱锥C-PBD的高.
分析 (Ⅰ)底面ABCD是边长为1的菱形,可得AC⊥BD,利用PA⊥平面ABCD,可得PA⊥BD,即可证明BD⊥平面PAC,进而证明平面PAC⊥平面PBD;
(Ⅱ)求出三棱锥P-BCD的体积,利用等体积,求三棱锥C-PBD的高.
解答  (Ⅰ)证明:∵四边形ABCD是菱形,∴AC⊥BD.…(1分)
(Ⅰ)证明:∵四边形ABCD是菱形,∴AC⊥BD.…(1分)
又∵PA⊥平面ABCD,BD?平面ABCD,
∴PA⊥BD.…(3分)
∵PA∩AC=A,∴BD⊥平面PAC…(4分)
∵BD?平面PBD,
∴平面PBD⊥平面PAC…(6分)
(Ⅱ)解:由$PA=\sqrt{3}$易得PB=PD=2,
∵ABCD是边长为1的菱形,且∠BAD=60°∴BD=1…(7分)
连PO,求得$PO=\frac{{\sqrt{15}}}{2}$…(8分)
∴${S_{△PBD}}=\frac{1}{2}×BD×PO=\frac{1}{2}×1×\frac{{\sqrt{15}}}{2}=\frac{{\sqrt{15}}}{4}$…(9分)
三棱锥P-BCD的体积${V_{P-BCD}}=\frac{1}{3}×{S_{△BCD}}×PA=\frac{1}{3}×\frac{{\sqrt{3}}}{4}×\sqrt{3}=\frac{1}{4}$…(10分)
设三棱锥C-PBD的高为h
则${V_{C-PBD}}={V_{P-BCD}}=\frac{1}{4}$,于是$\frac{1}{3}×\frac{{\sqrt{15}}}{4}×h=\frac{1}{4}$…(11分)
∴$h=\frac{{\sqrt{15}}}{5}$…(12分)
点评 本题考查了菱形的性质、线面垂直与面面垂直的判定性质定理、三棱锥的体积计算公式,考查了了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.PM 2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.根据现行国家标准GB3095-2012,PM 2.5日均值在35微克/立方米以下,空气质量为一级;在35微克/立方米~75微克/立方米之间,空气质量为二级;在75微克/立方米以上,空气质量为超标.从某自然保护区2014年全年每天的PM 2.5监测数据中随机地抽取10天的数据作为样本,监测值频数如下表所示:
(1)从这10天的PM 2.5日均值监测数据中,随机抽出3天,求恰有一天空气质量达到一级的概率;
(2)从这10天的数据中任取3天数据,记ξ表示抽到PM 2.5监测数据超标的天数,求ξ的分布列;
(3)以这10天的PM 2.5日均值来估计一年的空气质量情况,则一年(按365天计算)中平均有多少天的空气质量达到一级或二级(精确到整数).
| PM 2.5日均值(微克/立方米) | [25,35] | (35,45] | (45,55] | (55,65] | (65,75] | (75,85] |
| 频数 | 3 | 1 | 1 | 1 | 1 | 3 |
(2)从这10天的数据中任取3天数据,记ξ表示抽到PM 2.5监测数据超标的天数,求ξ的分布列;
(3)以这10天的PM 2.5日均值来估计一年的空气质量情况,则一年(按365天计算)中平均有多少天的空气质量达到一级或二级(精确到整数).
2.F为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1的右焦点,点P在双曲线右支上,△POF(O为坐标原点)是面积为$\sqrt{3}$的等边三角形,则双曲线的离心率为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\sqrt{3}$+1 |
9.下列函数中,周期为π,且在$[\frac{π}{4},\frac{π}{2}]$上为减函数的是( )
| A. | $y=cos(x+\frac{5π}{2})$ | B. | $y=cos(2x+\frac{5π}{2})$ | C. | $y=sin(x+\frac{5π}{2})$ | D. | $y=sin(2x+\frac{5π}{2})$ |
19.如图是一个几何体的三视图,则该几何体任意两个顶点间距离的最大值是( )
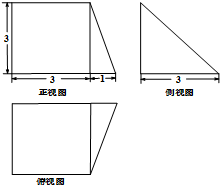

| A. | 3$\sqrt{2}$ | B. | 3$\sqrt{3}$ | C. | 4 | D. | 5 |
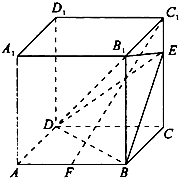 如图,在正方体ABCD一A1B1C1D1中,AB=3,CE=2EC1.
如图,在正方体ABCD一A1B1C1D1中,AB=3,CE=2EC1.