题目内容
11.已知a,b,x1,x2为正实数,且满足a+b=1(1)求a2+$\frac{b^2}{4}$的最小值.
(2)求证:(ax1+bx2)(bx1+ax2)≥x1x2.
分析 (1)由柯西不等式可得(a2+$\frac{b^2}{4}$)(1+4)≥(a+b)2,即${a^2}+\frac{b^2}{4}$≥$\frac{1}{5}$,从而可得${a^2}+\frac{b^2}{4}$的最小值;
(2)由柯西不等式可得$(a{x_1}+b{x_2})(b{x_1}+a{x_2})≥{(\sqrt{a{x_1}}\sqrt{a{x_2}}+\sqrt{b{x_1}}\sqrt{b{x_2}})^2}$,即可证明结论.
解答 (1)解:由柯西不等式可得(a2+$\frac{b^2}{4}$)(1+4)≥(a+b)2,∴${a^2}+\frac{b^2}{4}$≥$\frac{1}{5}$,
当$a=\frac{1}{5},b=\frac{4}{5}$时,${a^2}+\frac{b^2}{4}$的最小值为$\frac{1}{5}$;
(2)证明:由柯西不等式可得$(a{x_1}+b{x_2})(b{x_1}+a{x_2})≥{(\sqrt{a{x_1}}\sqrt{a{x_2}}+\sqrt{b{x_1}}\sqrt{b{x_2}})^2}$
=${(a\sqrt{{x_1}{x_2}}+b\sqrt{{x_1}{x_2}})^2}={(a+b)^2}{x_1}{x_2}={x_1}{x_2}$.
点评 本题考查柯西不等式的运用,考查学生分析解决问题的能力,正确运用柯西不等式是关键.

练习册系列答案
相关题目
1.已知四棱锥P-ABCD的底面四边形ABCD的对边互不平行,现用一平面α去截此四棱锥,且要使截面是平行四边形,则这样的平面α( )
| A. | 有且只有一个 | B. | 有四个 | C. | 有无数个 | D. | 不存在 |
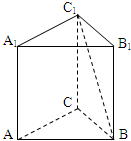 如图,在三棱柱ABC-A1B1C1中,底面是边长为1的正三角形,AA1⊥平面ABC,AA1=$\sqrt{2}$,则BC1与侧面ACC1A1所成的角的大小为$\frac{π}{6}$.
如图,在三棱柱ABC-A1B1C1中,底面是边长为1的正三角形,AA1⊥平面ABC,AA1=$\sqrt{2}$,则BC1与侧面ACC1A1所成的角的大小为$\frac{π}{6}$.