题目内容
16.如图,梯形ABCD中,CE⊥AD于E,BF⊥AD于F,且AF=BF=BC=1,DE=$\sqrt{2}$,现将△ABF,△CDE分别沿BF与CE翻折,使点A与点D重合.(Ⅰ)设面ABF与面CDE相交于直线l,求证:l∥CE;
(Ⅱ)试类比求解三角形的内切圆(与三角形各边都相切)半径的方法,求出四棱锥A-BCEF的内切球(与四棱锥各个面都相切)的半径.
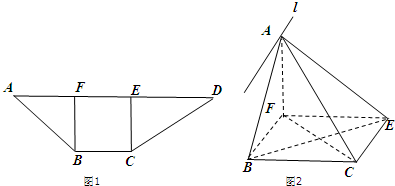
分析 (Ⅰ)由已知可得CE∥BF,由线面平行的判定定理得到CE与平面ABF平行,再由线面平行的性质定理得到l∥CE;
(Ⅱ)根据线面垂直的判定定理,可得AF⊥平面BCEF,故四棱锥A-BCEF是以平面BCEF为底面,以AF为高的棱锥,求出棱锥的体积,类比求解三角形的内切圆(与三角形各边都相切)半径的方法,可得答案.
解答 证明:(Ⅰ)∵CECE∥BF,CE?面ABF,BF?面ABF
∴CE∥面ABF
又∵CE?面ACE,面ABF∩面ACE=l.
∴l∥CE…(6分)
(Ⅱ)∵AF=BF=BC=1,DE=$\sqrt{2}$,
∴AE2=DE2=AF2+FE2,
即AF⊥EF,
又∵BF⊥AD于F,即AF⊥BF,EF,BF?平面BCEF,EF∩BF=F,
∴AF⊥平面BCEF,
故四棱锥A-BCEF是以平面BCEF为底面,以AF为高的棱锥,
故四棱锥A-BCEF的体积V=$\frac{1}{3}$×1×1×1=$\frac{1}{3}$,
四棱锥A-BCEF的表面积S=$\frac{1}{2}$(1+1+1+$\sqrt{2}$)×1+$\frac{1}{2}$×1×1+$\frac{1}{2}$×1×$\sqrt{2}$=2+$\sqrt{2}$,
类比求解三角形的内切圆(与三角形各边都相切)半径的方法,
设四棱锥A-BCEF的内切球半径为R,
则V=$\frac{1}{3}$SR,
故R=$\frac{2}{2+\sqrt{2}}$=$\frac{2-\sqrt{2}}{2}$
点评 本题考查了线面平行、类比推理及棱锥的体积表面积公式,是立体几何的简单综合应用,难度中档.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
1.调查某公司的四名推销员,其工作年限与年推销金额如表
由表中数据算出线性回归方程为$\stackrel{∧}{y}$=$\frac{67}{74}$x+$\stackrel{∧}{a}$.若该公司第五名推销员的工作年限为8年,则估计他(她)的年推销金额为$\frac{222}{37}$万元.
| 推销员编号 | 1 | 2 | 3 | 4 |
| 工作年限x/(年) | 3 | 5 | 10 | 14 |
| 年推销金额y/(万元) | 2 | 3 | 7 | 12 |
6.如图所示,当输入的实数x∈[2,30]时,执行如图所示的程序框图,则输出的x不小于111的概率是( )


| A. | $\frac{8}{13}$ | B. | $\frac{17}{28}$ | C. | $\frac{2}{3}$ | D. | $\frac{18}{29}$ |