题目内容
3.如图,菱形ABCD的边长为2,现将△ACD沿对角线AC折起至△ACP位置,并使平面PAC⊥平面ABC.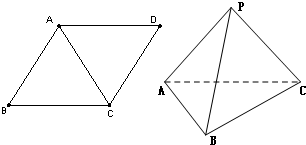
(Ⅰ)求证:AC⊥PB;
(Ⅱ)在菱形ABCD中,若∠ABC=60°,求直线AB与平面PBC所成角的正弦值;
(Ⅲ)求四面体PABC体积的最大值.
分析 (Ⅰ)取AC中点O,连接PO,BO,证明PO⊥AC,BO⊥AC,得到AC⊥平面POB,AC⊥PB.
(Ⅱ)以O为原点,以$\overrightarrow{OB},\overrightarrow{OC},\overrightarrow{OP}$方向分别为x,y,z轴正方向建立空间直角坐标系,求出平面PBC的法向量,然后求解直线AB与平面PBC成角的正弦值.
(Ⅲ)法一:设∠ABC=∠APC=α,α∈(0,π),求出体积的表达式,利用基本不等式求解四面体PABC体积的最大值.
法二:设∠ABC=∠APC=α,α∈(0,π),求出体积的表达式,利用函数的导数求解四面体PABC体积的最大值.
法三:设PO=x,则BO=x,$AC=2\sqrt{4-{x^2}}$,(0<x<2),求出体积的表达式,利用均值不等式求解四面体PABC体积的最大值.
解答 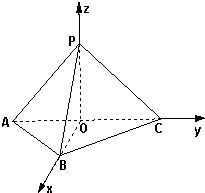 解:(Ⅰ)证明:取AC中点O,连接PO,BO,由于四边形ABCD为菱形,∴PA=PC,BA=BC,∴PO⊥AC,BO⊥AC,又PO∩BO=O,
解:(Ⅰ)证明:取AC中点O,连接PO,BO,由于四边形ABCD为菱形,∴PA=PC,BA=BC,∴PO⊥AC,BO⊥AC,又PO∩BO=O,
∴AC⊥平面POB,又PB?平面POB,∴AC⊥PB.
(Ⅱ)∵平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,PO?平面PAC,
PO⊥AC,∴PO⊥面ABC,∴OB,OC,OP两两垂直,
故以O为原点,以$\overrightarrow{OB},\overrightarrow{OC},\overrightarrow{OP}$方向分别为x,y,z轴正方向建立空间直角坐标系,∵∠ABC=60°,菱形ABCD的边长为2,
∴$A(0,-1,0),B(\sqrt{3},0,0),C(0,1,0),P(0,0,\sqrt{3})$,$\overrightarrow{AB}=(\sqrt{3},1,0),\overrightarrow{PB}=(\sqrt{3},0,-\sqrt{3}),\overrightarrow{PC}=(0,1,-\sqrt{3})$,
设平面PBC的法向量$\overrightarrow n=(x,y,z)$,直线AB与平面PBC成角为θ,
∴$\left\{\begin{array}{l}\sqrt{3}x-\sqrt{3}z=0\\ y-\sqrt{3}z=0\end{array}\right.$,取x=1,则$y=\sqrt{3},z=1$,于是$\overrightarrow n=(1,\sqrt{3},1)$,
∴$sinθ=|cos<\overrightarrow{AB},\overrightarrow n>|=|\frac{{\sqrt{3}+\sqrt{3}}}{{2•\sqrt{5}}}|=\frac{{\sqrt{15}}}{5}$,∴直线AB与平面PBC成角的正弦值为$\frac{{\sqrt{15}}}{5}$.
(Ⅲ)法一:
设∠ABC=∠APC=α,α∈(0,π),∴$PO=APcos\frac{α}{2}=2cos\frac{α}{2}$,${S_{△ABC}}=\frac{1}{2}•{2^2}sinα=2sinα$,
又PO⊥平面ABC,∴${V_{PABC}}=\frac{1}{3}{S_{△ABC}}•PO=\frac{4}{3}sinαcos\frac{α}{2}=\frac{8}{3}sin\frac{α}{2}{cos^2}\frac{α}{2}$=$\frac{8}{3}sin\frac{α}{2}({1-{{sin}^2}\frac{α}{2}})$
($0<\frac{α}{2}<\frac{π}{2}$),
∴${V^2}=\frac{32}{9}•2{sin^2}\frac{α}{2}({1-{{sin}^2}\frac{α}{2}})({1-{{sin}^2}\frac{α}{2}})$$≤\frac{32}{9}{({\frac{{2{{sin}^2}\frac{α}{2}+1-{{sin}^2}\frac{α}{2}+1-{{sin}^2}\frac{α}{2}}}{3}})^3}=\frac{32×2}{9×27}$,
∴$V≤\frac{{16\sqrt{3}}}{27}$,当且仅当$2{sin^2}\frac{α}{2}=1-{sin^2}\frac{α}{2}$,即$sin\frac{α}{2}=\frac{{\sqrt{3}}}{3}$时取等号,
∴四面体PABC体积的最大值为$\frac{{16\sqrt{3}}}{27}$.
法二:设∠ABC=∠APC=α,α∈(0,π),
∴$PO=APcos\frac{α}{2}=2cos\frac{α}{2}$,${S_{△ABC}}=\frac{1}{2}•{2^2}sinα=2sinα$,又PO⊥平面ABC,
∴${V_{PABC}}=\frac{1}{3}{S_{△ABC}}•PO=\frac{4}{3}sinαcos\frac{α}{2}=\frac{8}{3}sin\frac{α}{2}{cos^2}\frac{α}{2}$=$\frac{8}{3}sin\frac{α}{2}({1-{{sin}^2}\frac{α}{2}})$($0<\frac{α}{2}<\frac{π}{2}$),
设$t=sin\frac{α}{2}$,则${V_{PABC}}=\frac{8}{3}(t-{t^3})$,且0<t<1,
∴${V'_{PABC}}=\frac{8}{3}(1-3{t^2})$,
∴当$0<t<\frac{{\sqrt{3}}}{3}$时,V'PABC>0,当$\frac{{\sqrt{3}}}{3}<t<1$时,V'PABC<0,
∴当$t=\frac{{\sqrt{3}}}{3}$时,VPABC取得最大值$\frac{{16\sqrt{3}}}{27}$,∴四面体PABC体积的最大值为$\frac{{16\sqrt{3}}}{27}$.
法三:设PO=x,则BO=x,$AC=2\sqrt{4-{x^2}}$,(0<x<2)
又PO⊥平面ABC,
∴${V_{P-ABC}}=\frac{1}{3}PO•{S_{△ABC}}=\frac{1}{3}•x•\frac{1}{2}•x•2\sqrt{4-{x^2}}=\frac{1}{3}•{x^2}\sqrt{4-{x^2}}$,
∵$\frac{1}{3}•{x^2}\sqrt{4-{x^2}}=\frac{1}{3}\sqrt{\frac{1}{2}{x^2}•{x^2}({8-2{x^2}})}≤\frac{1}{3}\sqrt{\frac{1}{2}{{({\frac{{{x^2}+{x^2}+8-2{x^2}}}{3}})}^3}}=\frac{{16\sqrt{3}}}{27}$,
当且仅当x2=8-2x2,即$x=\frac{{2\sqrt{6}}}{3}$时取等号,∴四面体PABC体积的最大值为$\frac{{16\sqrt{3}}}{27}$.
点评 本题考查直线与平面垂直的判定定理以及性质定理的应用,直线与平面所成角的求法,几何体的体积的最值的求法,考查转化思想以及空间思维能力的培养.

| A. | (1,4] | B. | (0,1] | C. | [-1,1] | D. | (4,+∞) |