题目内容
1.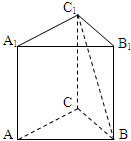 如图,在三棱柱ABC-A1B1C1中,底面是边长为1的正三角形,AA1⊥平面ABC,AA1=$\sqrt{2}$,则BC1与侧面ACC1A1所成的角的大小为$\frac{π}{6}$.
如图,在三棱柱ABC-A1B1C1中,底面是边长为1的正三角形,AA1⊥平面ABC,AA1=$\sqrt{2}$,则BC1与侧面ACC1A1所成的角的大小为$\frac{π}{6}$.
分析 取AC的中点D,连接BD,C1D,则∠BC1D是BC1与侧面ACC1A1所成的角,求出BD=$\frac{\sqrt{3}}{2}$,BC1=$\sqrt{3}$,即可得出结论.
解答 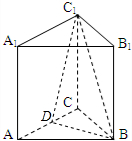 解:取AC的中点D,连接BD,C1D,则BD⊥AC,
解:取AC的中点D,连接BD,C1D,则BD⊥AC,
∵AA1⊥平面ABC,
∴AA1⊥BD,
∵AA1∩AC=A,
∴BD⊥平面ACC1A1,
∴∠BC1D是BC1与侧面ACC1A1所成的角,
∵底面是边长为1的正三角形,AA1=$\sqrt{2}$,
∴BD=$\frac{\sqrt{3}}{2}$,BC1=$\sqrt{3}$,
∴sin∠BC1D=$\frac{1}{2}$,
∴∠BC1D=$\frac{π}{6}$.
故答案为:$\frac{π}{6}$.
点评 本题考查直线与平面所成的角,考查学生的计算能力,正确作出直线与平面所成的角是关键.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
12.已知i为虚数单位,复数z满足1+i+(1+i)2z=(1-i)2,则复数z的虚部为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{2}i$ | C. | $\frac{3}{2}$ | D. | $-\frac{3}{2}$ |
10.已知函数y=ex,若f(x)的图象的一条切线经过点(-1,0),则这条切线与直线x=1及x轴所围成的三角形面积为( )
| A. | $\frac{2}{e}$ | B. | 1 | C. | 2 | D. | e |