题目内容
2.已知函数f(x)=ex(其中e是自然对数的底数),g(x)=x2+ax+1,a∈R.(1)记函数F(x)=f(x)•g(x),且a>0,求F(x)的单调增区间;
(2)若对任意x1,x2∈[0,2],x1≠x2,均有|f(x1)-f(x2)|>|g(x1)-g(x2)|成立,求实数a的取值范围.
分析 (1)因为F'(x)=ex[x+(a+1)](x+1),得出F(x)的单调区间.
(2)因为对任意x1,x2∈[0,2]且x1≠x2,均有|f(x1)-f(x2)|>|g(x1)-g(x2)|成立,根据f(x)=ex在[0,2]上的单调性,有$\left\{\begin{array}{l}f({x_1})+g({x_1})>f({x_2})+g({x_2})\\ f({x_1})-g({x_1})>f({x_2})-g({x_2})\end{array}\right.$对x1,x2∈[0,2],x1>x2恒成立,求解即可.
解答 解:(1)因为F(x)=f(x)•g(x)=ex(x2+ax+1),
所以F'(x)=ex[x+(a+1)](x+1),2分
令F'(x)>0,因为a>0,得x>-1或x<-(a+1),5分
所以F(x)的单调增区间为(-∞,-a-1)和(-1,+∞);6分
(2)因为对任意x1,x2∈[0,2]且x1≠x2,均有|f(x1)-f(x2)|>|g(x1)-g(x2)|成立,
不妨设x1>x2,根据f(x)=ex在[0,2]上单调递增,
所以有f(x1)-f(x2)>|g(x1)-g(x2)|对x1>x2恒成立,8分
所以f(x2)-f(x1)<g(x1)-g(x2)<f(x1)-f(x2)
对x1,x2∈[0,2],x1>x2恒成立,
即$\left\{\begin{array}{l}f({x_1})+g({x_1})>f({x_2})+g({x_2})\\ f({x_1})-g({x_1})>f({x_2})-g({x_2})\end{array}\right.$对x1,x2∈[0,2],x1>x2恒成立,
所以f(x)+g(x)和f(x)-g(x)在[0,2]都是单调递增函数,11分
当f'(x)+g'(x)≥0在[0,2]上恒成立,
得ex+(2x+a)≥0在[0,2]恒成立,得a≥-(ex+2x)在[0,2]恒成立,
因为-(ex+2x)在[0,2]上单调减函数,所以-(ex+2x)在[0,2]上取得最大值-1,
解得a≥-1. 13分
当f'(x)-g'(x)≥0在[0,2]上恒成立,
得ex-(2x+a)≥0在[0,2]上恒成立,即a≤ex-2x在[0,2]上恒成立,
因为ex-2x在[0,ln2]上递减,在[ln2,2]上单调递增,
所以ex-2x在[0,2]上取得最小值2-2ln2,
所以a≤2-2ln2,15分
所以实数a的取值范围为[-1,2-2ln2].16分
点评 本题主要考查了导数在求函数单调区间的应用和利用导数解决函数函数恒成立问题.属于难度较大题目.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{1}{2}$ | B. | $\frac{1}{2}i$ | C. | $\frac{3}{2}$ | D. | $-\frac{3}{2}$ |
| A. | $\frac{2}{e}$ | B. | 1 | C. | 2 | D. | e |
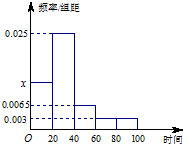 某学校随机抽取100名学生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].则该校学生上学所需时间的均值估计为33.6.(精确到1分钟)
某学校随机抽取100名学生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].则该校学生上学所需时间的均值估计为33.6.(精确到1分钟)