题目内容
【题目】已知函数f(x)= 
(1)当x≤0时,解不等式f(x)≥﹣1;
(2)写出该函数的单调区间;
(3)若函数g(x)=f(x)﹣m恰有3个不同零点,求实数m的取值范围.
【答案】
(1)解:当x≤0时, ![]() ,
,
解得x≥﹣1,
综上,﹣1≤x≤0,
故解集为[﹣1,0]
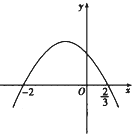
(2)解:函数f(x)的图象如右图,
函数f(x)的单调递减区间是(0,1),
单调增区间是(﹣∞,0)及(1,+∞)
(3)解:作出直线y=m,
函数g(x)=f(x)﹣m恰有3个不同零点等价于
函数y=m与函数f(x)的图象恰有三个不同公共点.
由函数 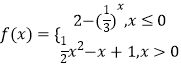
又f(0)=1, ![]() ,
,
∴ ![]() .
.
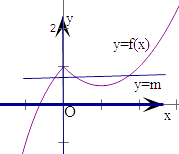
【解析】(1)由x≤0时的函数表达式,通过指数函数的单调性解出不等式即可;(2)画出函数f(x)的图象,通过图象观察即可;(3)作出直线y=m,函数g(x)=f(x)﹣m恰有3个不同零点等价于函数y=m与函数f(x)的图象恰有三个不同公共点.由图象观察即可得到.

练习册系列答案
相关题目