题目内容
【题目】定义在D上的函数f(x),如果满足:对任意x∈D,存在常数M>0,都有|f(x)|≤M成立,则称f(x)是D上的有界函数,其中M称为函数f(x)的上界.已知函数 ![]() .
.
(1)若f(x)是奇函数,求m的值;
(2)当m=1时,求函数f(x)在(﹣∞,0)上的值域,并判断函数f(x)在(﹣∞,0)上是否为有界函数,请说明理由;
(3)若函数f(x)在[0,1]上是以3为上界的函数,求实数m的取值范围.
【答案】
(1)解:由f(x)是奇函数,则f(﹣x)=﹣f(x)
得 ![]() ,即(1﹣m2)2x=0,∴m2﹣1=0,m=±1
,即(1﹣m2)2x=0,∴m2﹣1=0,m=±1
(2)解:当m=1时, ![]() .
.
∵x<0,∴0<2x<1,∴f(x)∈(0,1),满足|f(x)|≤1.
∴f(x)在(﹣∞,0)上为有界函数
(3)解:若函数f(x)在[0,1]上是以3为上界的有界函数,则有|f(x)|≤3在[0,1]上恒成立.
∴﹣3≤f(x)≤3,
即 ![]() ,
,
∴ 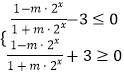 ,化简得:
,化简得:  ,
,
即 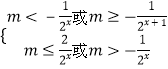 ,
,
上面不等式组对一切x∈[0,1]都成立,
故  ,
,
∴ ![]()
【解析】(1)根据函数奇偶性的性质建立方程关系进行求解即可.(2)根据分式函数的性质以及有界函数的定义进行求解判断即可.(3)根据函数的有界性建立不等式关系,利用不等式恒成立进行求解即可.

练习册系列答案
相关题目