Question

【题目】设f（x）=ax3+bx2+cx的极小值为﹣8，其导函数y=f′（x）的图象经过点 ，如图所示，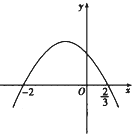
（1）求f（x）的解析式；
（2）若对x∈[﹣3，3]都有f（x）≥m2﹣14m恒成立，求实数m的取值范围．

Answer 1

【答案】
（1）解：∵f'（x）=3ax2+2bx+c，且y=f'（x）的图象经过点（﹣2，0）， ，

∴

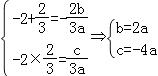
∴f（x）=ax3+2ax2﹣4ax，

由图象可知函数y=f（x）在（﹣∞，﹣2）上单调递减，在 上单调递增，在 上单调递减，

由f（x）极小值=f（﹣2）=a（﹣2）3+2a（﹣2）2﹣4a（﹣2）=﹣8，解得a=﹣1

∴f（x）=﹣x3﹣2x2+4x

（2）解：要使对x∈[﹣3，3]都有f（x）≥m2﹣14m恒成立，

只需f（x）min≥m2﹣14m即可．

由（1）可知函数y=f（x）在[﹣3，﹣2）上单调递减，在 上单调递增，在 上单调递减

且f（﹣2）=﹣8，f（3）=﹣33﹣2×32+4×3=﹣33＜﹣8

∴f（x）min=f（3）=﹣33（11分）﹣33≥m2﹣14m3≤m≤11

故所求的实数m的取值范围为{m|3≤m≤11}

【解析】（1）求出y=f'（x），因为导函数图象经过（﹣2，0）和（ ，0），代入即可求出a、b、c之间的关系式，再根据图象可知函数的单调性，而f（x）极小值为﹣8可得f（﹣2）=﹣8，解出即可得到a、b、c的值；（2）根据函数增减性求出函数在区间[﹣3，3]的最小值大于等于m2﹣14m，即可求出m的范围．
【考点精析】关于本题考查的函数的极值与导数，需要了解求函数的极值的方法是:（1）如果在附近的左侧,右侧,那么是极大值（2）如果在附近的左侧,右侧,那么是极小值才能得出正确答案．