题目内容
【题目】如图，在五面体ABCDPN中，棱PA⊥面ABCD，AB=AP=2PN，底面ABCD是菱形，∠BAD=
．
（1）求证：PN∥AB；
（2）求NC与平面BDN所成角的正弦值．
【答案】（1）见解析； （2）
.
【解析】
（1）菱形得线线平行，进而得线面平行，再得线线平行；
（2）需建立空间坐标系，找出相关点的坐标，利用公式计算得解．
（1）证明：
在菱形ABCD中，AB∥CD
∵CD面CDPN，AB面CDPN
∴AB∥面CDPN
又面ABNP∩面CDPN=PN
∴AB∥PN
（2）取CD中点M，
在菱形ABCD中，∠BAD=
，可知AM⊥AB
又PA⊥面ABCD
∴以A为原点建立空间坐标系如图
设AB=2，则B（2，0，0）
N（1，0，2），D（﹣1，
，0），C（1，，0）
∴
=（0，
，﹣2）
=（1，0，﹣2）
=（﹣3，，0）
设面BDN的法向量为
=（m，n，p）
则
，得
取m=2，则n=2，p=1
即
=（2，2，1）
设NC与平面BDN所成的角为θ，
则sinθ=|cos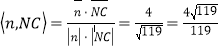
，
故NC与平面BDN所成角的正弦值为．
【题目】某零售店近5个月的销售额和利润额资料如下表：
商店名称 |
|
|
|
|
|
销售额 | 3 | 5 | 6 | 7 | 9 |
利润额 | 2 | 3 | 3 | 4 | 5 |
(1)画出散点图．观察散点图，说明两个变量有怎样的相关关系；
(2)用最小二乘法计算利润额
关于销售额
的回归直线方程；
(3)当销售额为4千万元时，利用(2)的结论估计该零售店的利润额(百万元)．
[参考公式：
，
]
【题目】一网站营销部为统计某市网友2017年12月12日在某网店的网购情况，随机抽查了该市60名网友在该网店的网购金额情况，如下表：
网购金额(单位：千元) | 频数 | 频率 | 网购金额(单位：千元) | 频数 | 频率 | |
[0,0.5) | 3 | 0.05 | [1.5,2) | 15 | 0.25 | |
[0.5,1) |
|
| [2,2.5) | 18 | 0.30 | |
[1,1.5) | 9 | 0.15 | [2.5,3] |
|
|
若将当日网购金额不小于2千元的网友称为“网购达人”，网购金额小于2千元的网友称为“网购探者”，已知“网购达人”与“网购探者”人数的比例为2:3.
（1）确定
，
，
，
的值，并补全频率分布直方图；
（2）①.试根据频率分布直方图估算这60名网友当日在该网店网购金额的平均数和中位数；
②.若平均数和中位数至少有一个不低于2千元，则该网店当日评为“皇冠店”，试判断该网店当日能否被评为“皇冠店”.
