题目内容
【题目】已知三次函数f（x）=x3+bx2+cx+d（a，b，c∈R）过点（3，0），且函数f（x）在点（0，f（0））处的切线恰好是直线y=0．
（1）求函数f（x）的解析式；
（2）设函数g（x）=9x+m﹣1，若函数y=f（x）﹣g（x）在区间[﹣2，1]上有两个零点，求实数m的取值范围．
【答案】
（1）解：f′（x）=3x2+2bx+c，由已知条件得：
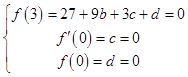，解得b=﹣3，c=d=0；
∴f（x）=x3﹣3x2
（2）解：由已知条件得：f（x）﹣g（x）=0在[﹣2，1]上有两个不同的解；
即x3﹣3x2﹣9x﹣m+1=0在区间[﹣2，1]有两个不同的解；
即m=x3﹣3x2﹣9x+1在[﹣2，1]上有两个不同解．
令h（x）=x3﹣3x2﹣9x+1，h′（x）=3x2﹣6x﹣9，x∈[﹣2，1]；
解3x2﹣6x﹣9＞0得：﹣2≤x＜﹣1；解3x2﹣6x﹣9＜0得：﹣1＜x≤1；
∴h（x）max=h（﹣1）=6，又f（﹣2）=﹣1，f（1）=﹣10，∴h（x）min=﹣10；
m=h（x）在区间[﹣2，1]上有两个不同的解，∴﹣1≤m＜6．
∴实数m的取值范围是[﹣1，6）
【解析】（1）根据已知条件即可建立关于b，c，d的三个方程，解方程即可求出b，c，d，从而求出f（x）的解析式．（2）由已知条件可得到方程f（x）﹣g（x）=0在区间[﹣2，1]上有两个不同的解，带入f（x），g（x）后得到：方程x3﹣3x2﹣9x﹣m+1=0在区间[﹣2，1]上有两个不同解．因为求m的取值范围，所以把方程变成：m=x3﹣3x2﹣9x+1，求函数x3﹣3x2﹣9x+1在区间[﹣2，1]上的取值范围，要使方程有两个不同的解，从而求出m应满足的范围．这样便求出了m的取值范围．
【考点精析】解答此题的关键在于理解函数的最大(小)值与导数的相关知识，掌握求函数
在
上的最大值与最小值的步骤：（1）求函数在
内的极值；（2）将函数的各极值与端点处的函数值
，
比较，其中最大的是一个最大值，最小的是最小值．
阅读快车系列答案【题目】在一次耐力和体能测试之后，某校对其甲、乙、丙、丁四位学生的耐力成绩（
）和体能成绩（
）进行回归分析，求得回归直线方程为
．由于某种原因，成绩表（如下表所示）中缺失了乙的耐力和体能成绩．
甲 | 乙 | 丙 | 丁 | |
耐力成绩(X) | 7.5 | m | 8 | 8.5 |
体能成绩(Y) | 8 | n | 8.5 | 9.5 |
综合素质 （ | 15.5 | 16 | 16.5 | 18 |
（Ⅰ）请设法还原乙的耐力成绩
和体能成绩
；
（Ⅱ）在区域性校际学生身体综合素质比赛中，由甲、乙、丙、丁四位学生组成学校代表队参赛.共举行3场比赛，每场比赛均由赛事主办方从学校代表中随机抽两人参赛，每场比赛所抽的选手中，只要有一名选手的综合素质分高于16分，就能为所在学校赢得一枚荣誉奖章．若记比赛中赢得荣誉奖章的枚数为
，试根据上表所提供数据，预测该校所获奖章数
的分布列与数学期望．
