题目内容
已知正方形 ABCD所在平面与正方形ABEF所在平面互相垂直,M为AC上一点,N为BF 上一点,且
ABCD所在平面与正方形ABEF所在平面互相垂直,M为AC上一点,N为BF 上一点,且 有,设
有,设
(1) 求证: ;
;
(2) 求证: ;
;
(3) 当 为何值时,
为何值时, 取最小值?并求出这个最小值.
取最小值?并求出这个最小值.
 ABCD所在平面与正方形ABEF所在平面互相垂直,M为AC上一点,N为BF 上一点,且
ABCD所在平面与正方形ABEF所在平面互相垂直,M为AC上一点,N为BF 上一点,且 有,设
有,设
(1) 求证:
 ;
;(2) 求证:
 ;
;(3) 当
 为何值时,
为何值时, 取最小值?并求出这个最小值.
取最小值?并求出这个最小值.(1)证明略
(2)证明略
(3)
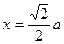
证明:
(1) 在平面ABC中,作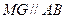 ,在平面BFE中,作
,在平面BFE中,作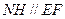 ,连结GH
,连结GH
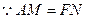
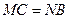
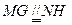
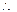 MNHG为平行四
MNHG为平行四 边形;
边形;
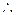
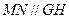
又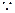 GH
GH 面BEC,MN
面BEC,MN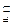
 面BEC
面BEC
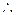 MN//面BEC
MN//面BEC
(2)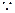
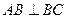
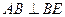
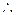 AB
AB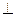 面BEC
面BEC
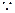 GH
GH 面GEC
面GEC 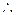 AB
AB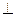 GH
GH
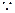 MN//GH
MN//GH 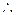 MN
MN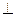 AB
AB
(3)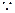 面ABCD
面ABCD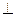 面ABEF
面ABEF
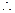 BE
BE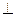 面ABCD
面ABCD 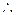 BE
BE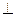 BC
BC
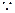 BG=
BG=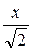 , BH=
, BH=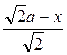
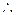 MN=GH=
MN=GH=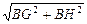 =
=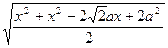
=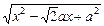 (
(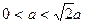 )
)
=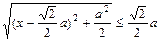 当且仅当
当且仅当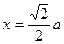 时,等号成立;
时,等号成立;
(1) 在平面ABC中,作
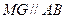 ,在平面BFE中,作
,在平面BFE中,作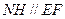 ,连结GH
,连结GH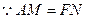
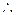
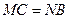
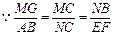
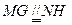
 MNHG为平行四
MNHG为平行四 边形;
边形;
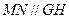
又
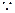 GH
GH 面BEC,MN
面BEC,MN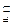
 面BEC
面BEC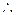 MN//面BEC
MN//面BEC (2)
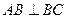
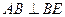
 AB
AB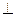 面BEC
面BEC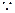 GH
GH 面GEC
面GEC 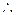 AB
AB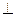 GH
GH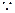 MN//GH
MN//GH 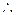 MN
MN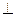 AB
AB(3)
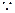 面ABCD
面ABCD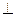 面ABEF
面ABEF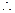 BE
BE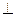 面ABCD
面ABCD 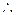 BE
BE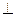 BC
BC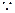 BG=
BG=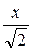 , BH=
, BH=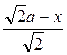
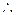 MN=GH=
MN=GH=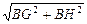 =
=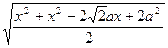
=
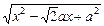 (
(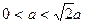 )
)=
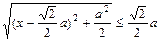 当且仅当
当且仅当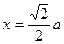 时,等号成立;
时,等号成立;
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 试用反证法证明三条抛物线中至少有一条与x轴的交点不只一个。
试用反证法证明三条抛物线中至少有一条与x轴的交点不只一个。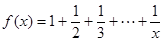 ,计算得当
,计算得当 时
时 ,当
,当 时有
时有 ,
, ,
, ,
, ,因此猜测当
,因此猜测当
 -
- ≥a+
≥a+ -2.
-2.
 ,…,可归纳出式子( )
,…,可归纳出式子( )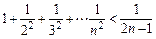



 没有最小数”时,可用反证法证明.
没有最小数”时,可用反证法证明. 是
是 中的最小数,则取
中的最小数,则取 ,可得:
,可得: ,与假设中“
,与假设中“ 是
是 没有最大数”,也可以用反证法证明.我们可以假设
没有最大数”,也可以用反证法证明.我们可以假设 是
是 中的最大数,则可以找到
中的最大数,则可以找到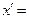 ▲ (用
▲ (用 ,
, 表示),由此可知
表示),由此可知 ,
, ,这与假设矛盾!所以数集
,这与假设矛盾!所以数集