题目内容
4.号码为1,2,3的三个球放在一个缸子中,将一个球从缸子中取出,把它的号码记下来,然后再将它放回到缸子里,这个过程重复三次,每个球在每次过程中被取出的机会是等可能的,如果记录的数码之和为6,那么其中号码为2的球三次全被取出的概率为$\frac{1}{7}$.分析 先求出所有的基本事件,再找到满足条件的(2,2,2)只有一种,根据概率公式计算即可.
解答 解:根据题意,从袋中依次有放回的取三次球,记录的数码之和为6,共有(1,2,3),(1,3,2),(2,3,1),(2,1,3),(3,2,1),(3,1,2),(2,2,2)
,那么其中号码为2的球三次全被取出,只有(2,2,2)一种情况,
故其中号码为2的球三次全被取出的概率为:$\frac{1}{7}$
故答案为:$\frac{1}{7}$
点评 本题考查条件概率计算公式,考查学生的计算能力,比较基础.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
11.与直线x-y+4=0和圆x2+y2-2x+2y=0都相切的半径最小的圆的方程是( )
| A. | (x+1)2+(y+1)2=2 | B. | (x+1)2+(y-1)2=2 | C. | (x+1)2+(y+1)2=4 | D. | (x+1)2+(y-1)2=4 |
8.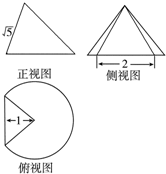 一个圆锥被过顶点的平面截去了较小的一部分,余下的几何体的三视图如图,则该几何体的表面积为( )
一个圆锥被过顶点的平面截去了较小的一部分,余下的几何体的三视图如图,则该几何体的表面积为( )
 一个圆锥被过顶点的平面截去了较小的一部分,余下的几何体的三视图如图,则该几何体的表面积为( )
一个圆锥被过顶点的平面截去了较小的一部分,余下的几何体的三视图如图,则该几何体的表面积为( )| A. | $\sqrt{5}$+$\frac{3\sqrt{3}π}{2}$+$\frac{3π}{2}$+1 | B. | 2$\sqrt{5}$+3$\sqrt{3}$π+$\frac{3π}{2}$+1 | C. | $\sqrt{5}$+$\frac{3\sqrt{3}π}{2}$+$\frac{3π}{2}$ | D. | $\sqrt{5}$+$\frac{3\sqrt{3}π}{2}$+$\frac{π}{2}$+1 |