题目内容
4.下面四个图象中,有一个是函数f(x)=$\frac{1}{3}$x3+ax2+(a2-1)x+1(a∈R)的导函数y=f'(x)的图象,则f(-1)等于( )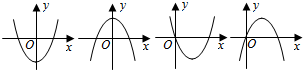
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{5}{3}$ | D. | -$\frac{1}{3}$或$\frac{5}{3}$ |
分析 先求出f′(x),根据开口方向,对称轴,判断哪一个图象是导函数y=f′(x)的图象,再根据图象求出a的值,最后求出f(-1).
解答 解:函数的f(x)的导数f′(x)=x2+2ax+(a2-1)=(x+a)2-1,
则f′(x)的图象开口向上,排除(2)(4),
若是(1)则,对称轴关于y轴对称,则2a=0,即a=0,
f(x)=$\frac{1}{3}$x3-x+1,
∴f(-1)=-$\frac{1}{3}$+1+1=$\frac{5}{3}$,
若对应的图象应为(3),
则函数过原点,a2-1=0,解得a=1,或a=-1且对称轴x=-a>0,即a<0,
∴a=-1
∴f(x)=$\frac{1}{3}$x3-x2+1,
∴f(-1)=-$\frac{1}{3}$-1+1=-$\frac{1}{3}$,
故选:D.
点评 本题主要考查函数图象的确定,以及导数的基本运算,属于基础题.

练习册系列答案
相关题目
15.函数f(x)是定义在R上的奇函数,且f(1)=0,当x>0时,有$\frac{xf′(x)-f(x)}{{x}^{2}}$>0恒成立,则不等式f(x)>0的解集为( )
| A. | (-1,0)∪(1,+∞) | B. | (-1,0)∪(0,1) | C. | (-∞,-1)∪(1,+∞) | D. | (-∞,-1)∪(0,1) |
12.用秦九韶算法计算多项式f(x)=12+35x+9x3+5x5+3x6,在当x=-1时的值,有如下的说法:①要用到6次乘法和6次加法;②要用到6次加法和8次乘法;③v0=-23; ④v3=11,其中正确的是( )
| A. | ①③ | B. | ①④ | C. | ②④ | D. | ①③④ |
16.已知函数f(x)=$\left\{\begin{array}{l}\frac{1}{x+2},-1≤x≤0\\{x}^{2}-2x,0<x≤1\end{array}\right.$,若f(2m-1)<$\frac{1}{2}$,则m的取值范围是( )
| A. | m>$\frac{1}{2}$ | B. | m$<\frac{1}{2}$ | C. | 0$≤m<\frac{1}{2}$ | D. | $\frac{1}{2}<m≤1$ |
13.A={x|x<1},B={x|x<-2或x>0},则A∩B=( )
| A. | (0,1) | B. | (-∞,-2) | C. | (-2,0) | D. | (-∞,-2)∪(0,1) |