题目内容
16.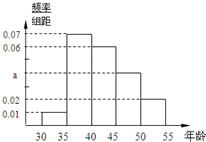 某同学对本地[30,55]岁的爱好阅读的人群随机抽取n人进行了一次调查,得到如下年龄统计表,其中不超过40岁的共有60人.
某同学对本地[30,55]岁的爱好阅读的人群随机抽取n人进行了一次调查,得到如下年龄统计表,其中不超过40岁的共有60人.(1)求出n,a的值;
(2)从[45,55)岁年龄段爱好阅读的人中采用分层抽样法抽取6人,然后从这6人之中选2人为社区阅读大使,求选出的两人年龄均在[45,50)内的概率.
分析 (1)根据题意,其中不超过40岁的共有60人求出n的值,结合直方图,计算可得a值;
(2)先有分层抽样方法可得各个年龄段的人数,设a1、a2、a3、a4为[40,50)岁中抽得的4人,b1、b2为[50,55)岁中抽得的2人,进而用列举法可得抽出2人的全部情况,由古典概型公式计算可得答案.
解答 解(1)不超过40所所占的比例为5(0.01+0.07)=0.4,
所以0.4n=60,解得n=150,
1=5(0.01+0.02+a+0.06+0.07),
解得a=0.04
(2)因为[45,50)岁年龄段的爱好阅读的共有30人,[50,55)岁年龄段的爱好阅读的共有15人,
所以分层抽样时,在[45,50)抽4人,在[50,55)抽2人,
设a1、a2、a3、a4为[40,50)岁中抽得的4人,b1、b2为[50,55)岁中抽得的2人,
全部可能的结果有:(a1,a2),( a1,a3),( a1,a4),( a1,b1),( a1,b2),(a2,a3),(a2,a4),(a2,b1),(a2,b2),(a3,a4),(a3,b1),(a3,b2),(a4,b1),(a4,b2),(b1,b2),共15个,
而选出的两人年龄均在[45,50)内有6个,
故选出的两人年龄均在[45,50)内的概率P=$\frac{6}{15}$=$\frac{2}{5}$.
点评 本题考查频率分步直方图的画法、应用以及列举法求古典概型,关键是掌握频率分步直方图意义以及运算.

练习册系列答案
相关题目
6.已知点(1,-2)和$({\frac{{\sqrt{3}}}{3},0})$在直线l:ax-y-1=0(a≠0)的两侧,则直线l倾斜角的取值范围是( )
| A. | $({\frac{π}{4},\frac{π}{3}})$ | B. | $({\frac{2π}{3},\frac{5π}{6}})$ | C. | $({0,\frac{π}{3}})∪({\frac{3π}{4},π})$ | D. | $({\frac{π}{3},\frac{2π}{3}})$ |
4.设全集U=R,集合R={0,1,2},B={x|$\frac{1}{x-1}$>0,x∈R},则A∩∁UB=( )
| A. | {0} | B. | {0,1} | C. | {1,2} | D. | {0,1,2} |
11.若$cos(\frac{π}{6}-α)=m,(|m|≤1)$,则$sin(\frac{2π}{3}-α)$的值为( )
| A. | -m | B. | $-\frac{m}{2}$ | C. | $\frac{m}{2}$ | D. | m |
8.某饮料销售点销售某品牌饮料,饮料的零售价x(元/瓶)与销量y(瓶)的关系统计如下:
由表中数据得线性回归方程:$\widehat{y}$=-20x+a,当零售价为每瓶3.7元时,估计该销售点销售的这种饮料的瓶数为( )
| 零售价x(元/瓶) | 3.0 | 3.2 | 3.4 | 3.6 | 3.8 | 4.0 |
| 销量y(瓶) | 50 | 44 | 43 | 40 | 35 | 28 |
| A. | 39 | B. | 38 | C. | 37 | D. | 36 |
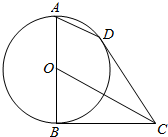 如图所示,AB为圆O的直径,BC,CD为圆O的切线,B,D为切点.
如图所示,AB为圆O的直径,BC,CD为圆O的切线,B,D为切点.