题目内容
7.已知函数f(x)=|2x-1|(1)解关于x的不等式f(x)≥3;
(2)若方程f(x)+|x-2|=ax在[1,+∞)上有解,求实数a的取值范围.
分析 (1)关于x的不等式即|2x-1|≥3,由此求得不等式的解集.
(2)f(x)+|x-2|=$\left\{\begin{array}{l}{3x-3,x≥2}\\{x+1,1≤x<2}\end{array}\right.$,分类讨论,分别求得a的范围,再取并集,即得所求.
解答 解:(1)关于x的不等式f(x)≥3,即|2x-1|≥3,即2x-1≥3 或2x-1≤-3.
求得x≥2 或x≤-1,故要求的不等式的解集为{x|x≥2 或x≤-1 }.
(2)f(x)+|x-2|=$\left\{\begin{array}{l}{3x-3,x≥2}\\{x+1,1≤x<2}\end{array}\right.$,当x≥2时,方程即3x-3=ax,即a=3-$\frac{3}{x}$,$a∈[\frac{3}{2},3)$.
当1≤x<2时,方程即 x+1=ax,即 a=1+$\frac{1}{x}$,∴a∈($\frac{3}{2}$,2].
综上,a∈[$\frac{3}{2}$,3).
点评 本题主要考查绝对值不等式的解法,体现了等价转化和分类讨论的数学思想,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.用合适的方法证明下面两个问题:
(1)设a≥b>0,求证:2a3-b3≥2ab2-a2b;
(2)设a>0,b>0,且a+b=10,求证:$\sqrt{1+3a}$+$\sqrt{1+3b}$≤8.
(1)设a≥b>0,求证:2a3-b3≥2ab2-a2b;
(2)设a>0,b>0,且a+b=10,求证:$\sqrt{1+3a}$+$\sqrt{1+3b}$≤8.
17.设m、n为两条不重合的直线,α,β为两个不重合的平面,下列命题中正确的是( )
| A. | 若m、n与α所成的角相等,则m∥n | B. | 若n∥α,m∥β,α∥β,则m∥n | ||
| C. | 若n?α,m?β,m∥n,则α∥β | D. | 若n⊥α,m⊥β,α⊥β,则n⊥m |
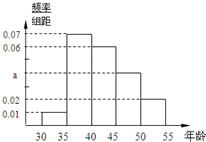 某同学对本地[30,55]岁的爱好阅读的人群随机抽取n人进行了一次调查,得到如下年龄统计表,其中不超过40岁的共有60人.
某同学对本地[30,55]岁的爱好阅读的人群随机抽取n人进行了一次调查,得到如下年龄统计表,其中不超过40岁的共有60人.