题目内容
4.设全集U=R,集合R={0,1,2},B={x|$\frac{1}{x-1}$>0,x∈R},则A∩∁UB=( )| A. | {0} | B. | {0,1} | C. | {1,2} | D. | {0,1,2} |
分析 求出集合B中的不等式的解集,确定出集合B,根据全集U=R,找出集合B的补集,然后找出集合B补集与集合A的公共元素,即可求出所求的集合
解答 解:由集合B中的不等式$\frac{1}{x-1}$>0,
解得:x>1
∴B=(1,+∞),又全集U=R,
∴CUB=(-∞,1],又A={0,1,2},
∴A∩CUB={0,1}.
故选:B.
点评 此题考查了交、并、补集的混合运算,是一道基本题型,求集合补集时注意全集的范围.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
13.下列推理所得结论正确的是( )
| A. | 由a(b+c)=ab+ac类比得到loga(x+y)=logax+logby | |
| B. | 由a(b+c)=ab+ac类比得到cos(x+y)=cosx+cosy | |
| C. | 由(a+b)c=ac+bc类比$\frac{a+b}{c}$=$\frac{a}{c}$+$\frac{b}{c}$(c≠0) | |
| D. | 由(ab)n=anbn类比得到(x+y)n=xn+yn |
14.下列结论正确的是( )
| A. | 若ac>bc,则a>b | B. | 若a2>b2,则a>b | ||
| C. | 若a>b,c>d,则ac>bd | D. | 若a>b>0,则a>$\frac{a+b}{2}>\sqrt{ab}$>b |
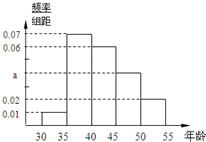 某同学对本地[30,55]岁的爱好阅读的人群随机抽取n人进行了一次调查,得到如下年龄统计表,其中不超过40岁的共有60人.
某同学对本地[30,55]岁的爱好阅读的人群随机抽取n人进行了一次调查,得到如下年龄统计表,其中不超过40岁的共有60人.