题目内容
6.若不等式|x-3|+|x+1|>a恒成立,则a的取值范围为(-∞,4).分析 由条件利用绝对值三角不等式求得|x-3|+|x+1|的最小值,从而得到a的取值范围.
解答 解:(1)∵|x-3|+|x+1|≥|(x-3)-(x+1)|=4,|x-3|+|x+1|>a恒成立,
∴4>a恒成立,即 a<4,
故答案为:(-∞,4).
点评 本题主要考查绝对值三角不等式,绝对值不等式的解法,体现了转化的数学思想,属于基础题.

练习册系列答案
相关题目
17.设m、n为两条不重合的直线,α,β为两个不重合的平面,下列命题中正确的是( )
| A. | 若m、n与α所成的角相等,则m∥n | B. | 若n∥α,m∥β,α∥β,则m∥n | ||
| C. | 若n?α,m?β,m∥n,则α∥β | D. | 若n⊥α,m⊥β,α⊥β,则n⊥m |
14.下列结论正确的是( )
| A. | 若ac>bc,则a>b | B. | 若a2>b2,则a>b | ||
| C. | 若a>b,c>d,则ac>bd | D. | 若a>b>0,则a>$\frac{a+b}{2}>\sqrt{ab}$>b |
11.函数f(x)=sin2x+4cosx+2的值域为( )
| A. | (-∞,3] | B. | [-2,6] | C. | [-2,7] | D. | (-∞,7] |
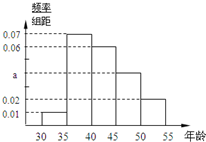 某同学对本地[30,55]岁的爱好阅读的人群随机抽取n人进行了一次调查,得到如下年龄统计表,其中不超过40岁的共有60人.
某同学对本地[30,55]岁的爱好阅读的人群随机抽取n人进行了一次调查,得到如下年龄统计表,其中不超过40岁的共有60人.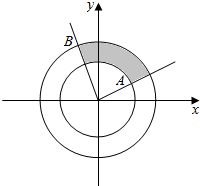 如图,两同心圆(圆心在原点)分别与OA、OB交于A、B两点,其中A($\sqrt{2}$,1),|OB|=$\sqrt{6}$,阴影部分为两同心圆构成的扇环,已知扇环的面积为$\frac{π}{2}$.
如图,两同心圆(圆心在原点)分别与OA、OB交于A、B两点,其中A($\sqrt{2}$,1),|OB|=$\sqrt{6}$,阴影部分为两同心圆构成的扇环,已知扇环的面积为$\frac{π}{2}$.