题目内容
1.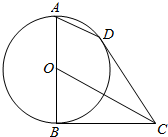 如图所示,AB为圆O的直径,BC,CD为圆O的切线,B,D为切点.
如图所示,AB为圆O的直径,BC,CD为圆O的切线,B,D为切点.(Ⅰ)求证:AB∥OC;
(Ⅱ)若圆O的半径为2,求AD•OC的值.
分析 (Ⅰ)要证明AD∥OC,我们要根据直线平行的判定定理,观察已知条件及图形,我们可以连接OD,构造出内错角,只要证明∠1=∠3即可得证.
(Ⅱ)因为⊙O的半径为1,而其它线段长均为给出,故要想求AD•OC的值,我们要将其转化用半径相等或相关的线段积的形式,结合(Ⅰ)的结论,我们易证明Rt△BAD∽Rt△ODC,根据相似三角形性质,不们不难得到转化的思路.
解答 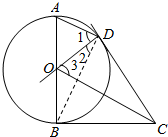 (Ⅰ)证明:如图,连接BD、OD.
(Ⅰ)证明:如图,连接BD、OD.
∵CB、CD是⊙O的两条切线,
∴BD⊥OC,
∴∠2+∠3=90°
又AB为⊙O直径,∴AD⊥DB,
∠1+∠2=90°,
∴∠1=∠3,
∴AD∥OC;
(Ⅱ)解:AO=OD,则∠1=∠A=∠3,
∴Rt△BAD∽Rt△ODC,
∵圆O的半径为2,
∴AD•OC=AB•OD=8.
点评 根据求证的结论,使用分析推敲证明过程中所需要的条件,进而分析添加辅助线的方法,是平面几何证明必须掌握的技能,大家一定要熟练掌握,而在(Ⅱ)中根据已知条件分析转化的方向也是解题的主要思想.解决就是寻找解题的思路,由已知出发,找寻转化方向和从结论出发寻找转化方向要结合在一起使用.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
13.下列推理所得结论正确的是( )
| A. | 由a(b+c)=ab+ac类比得到loga(x+y)=logax+logby | |
| B. | 由a(b+c)=ab+ac类比得到cos(x+y)=cosx+cosy | |
| C. | 由(a+b)c=ac+bc类比$\frac{a+b}{c}$=$\frac{a}{c}$+$\frac{b}{c}$(c≠0) | |
| D. | 由(ab)n=anbn类比得到(x+y)n=xn+yn |
10.根据如下样本数据:
得到的回归方程为$\overrightarrow{y}$=$\overrightarrow{b}$x+$\overrightarrow{a}$,则( )
| x | 3 | 4 | 5 | 6 | 7 | 8 |
| y | 10 | 9 | 7 | 6 | 4 | 3 |
| A. | $\overrightarrow{a}$>0,$\overrightarrow{b}$>0 | B. | $\overrightarrow{a}$>0,$\overrightarrow{b}$<0 | C. | $\overrightarrow{a}$<0,$\overrightarrow{b}$>0 | D. | $\overrightarrow{a}$<0,$\overrightarrow{b}$<0 |
11.函数f(x)=sin2x+4cosx+2的值域为( )
| A. | (-∞,3] | B. | [-2,6] | C. | [-2,7] | D. | (-∞,7] |
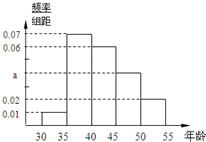 某同学对本地[30,55]岁的爱好阅读的人群随机抽取n人进行了一次调查,得到如下年龄统计表,其中不超过40岁的共有60人.
某同学对本地[30,55]岁的爱好阅读的人群随机抽取n人进行了一次调查,得到如下年龄统计表,其中不超过40岁的共有60人.