题目内容
6.已知点(1,-2)和$({\frac{{\sqrt{3}}}{3},0})$在直线l:ax-y-1=0(a≠0)的两侧,则直线l倾斜角的取值范围是( )| A. | $({\frac{π}{4},\frac{π}{3}})$ | B. | $({\frac{2π}{3},\frac{5π}{6}})$ | C. | $({0,\frac{π}{3}})∪({\frac{3π}{4},π})$ | D. | $({\frac{π}{3},\frac{2π}{3}})$ |
分析 因为点(1,-2)和$({\frac{{\sqrt{3}}}{3},0})$在直线l:ax-y-1=0(a≠0)的两侧,那么把这两个点代入ax-y-1,它们的符号相反,乘积小于0,求出a的范围,设直线l倾斜角为θ,则a=tanθ,再根据正切函数的图象和性质即可求出范围.
解答 解:因为点(1,-2)和$({\frac{{\sqrt{3}}}{3},0})$在直线l:ax-y-1=0(a≠0)的两侧,
所以,(a+2-1)($\frac{\sqrt{3}}{3}$a-1)<0,
即:(a+1)(a-$\sqrt{3}$)<0,
解得-1<a<$\sqrt{3}$,
设直线l倾斜角为θ,
∴a=tanθ,
∴-1<tanθ<$\sqrt{3}$,
∴0<θ<$\frac{π}{3}$,或$\frac{3π}{4}$<θ<π,
故选:C.
点评 本题考查二元一次不等式组与平面区域问题,点与直线的位置关系,是中档题.

练习册系列答案
相关题目
16.若函数f(x)=sinωx+$\sqrt{3}$cosωx(ω>0)的最小正周期为π,则它的图象的一个对称中心为( )
| A. | ($\frac{π}{2}$,0) | B. | ($\frac{π}{3}$,0) | C. | ($\frac{π}{6}$,0) | D. | ($\frac{π}{12}$,0) |
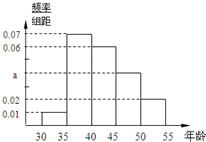 某同学对本地[30,55]岁的爱好阅读的人群随机抽取n人进行了一次调查,得到如下年龄统计表,其中不超过40岁的共有60人.
某同学对本地[30,55]岁的爱好阅读的人群随机抽取n人进行了一次调查,得到如下年龄统计表,其中不超过40岁的共有60人.