题目内容
已知 为二次函数,不等式
为二次函数,不等式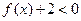 的解集为
的解集为 ,且对任意
,且对任意 ,恒有
,恒有 .
.
数列 满足
满足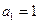 ,
,
 .
.
(1) 求函数 的解析式;
的解析式;
(2) 设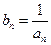 ,求数列
,求数列 的通项公式;
的通项公式;
(3) 若(2)中数列 的前
的前 项和为
项和为 ,求数列
,求数列 的前
的前 项和
项和 .
.
 为二次函数,不等式
为二次函数,不等式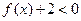 的解集为
的解集为 ,且对任意
,且对任意 ,恒有
,恒有 .
. 数列
 满足
满足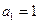 ,
,
 .
.(1) 求函数
 的解析式;
的解析式;(2) 设
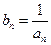 ,求数列
,求数列 的通项公式;
的通项公式;(3) 若(2)中数列
 的前
的前 项和为
项和为 ,求数列
,求数列 的前
的前 项和
项和 .
. (1) (2)
(2)
(3)
 (2)
(2)
(3)

(1) 依题设,
 ,即
,即 .…2分
.…2分
令 ,则
,则 ,有
,有 ,得
,得 . …………4分
. …………4分
即 ,得
,得 .
.
∴ . …………5分
. …………5分
(2) ,则
,则 ,即
,即 …6分
…6分
两边取倒数,得 ,即
,即 . …………7分
. …………7分
∴数列 是首项为
是首项为 ,公差为
,公差为 的等差数列. …………8分
的等差数列. …………8分
∴
 . …………9分
. …………9分
(3) ∵ , …………10分
, …………10分
∴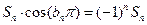 .
.
∴ .
.
①当 为偶数时,
为偶数时,

 . …………12分
. …………12分
②当 为奇数时,
为奇数时,
 .
.
综上, . …………14分
. …………14分

 ,即
,即 .…2分
.…2分令
 ,则
,则 ,有
,有 ,得
,得 . …………4分
. …………4分即
 ,得
,得 .
.∴
 . …………5分
. …………5分(2)
 ,则
,则 ,即
,即 …6分
…6分两边取倒数,得
 ,即
,即 . …………7分
. …………7分∴数列
 是首项为
是首项为 ,公差为
,公差为 的等差数列. …………8分
的等差数列. …………8分∴

 . …………9分
. …………9分(3) ∵
 , …………10分
, …………10分∴
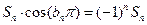 .
. ∴
 .
. ①当
 为偶数时,
为偶数时,
 . …………12分
. …………12分②当
 为奇数时,
为奇数时, .
. 综上,
 . …………14分
. …………14分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
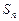 是数列
是数列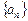 的前n项和,
的前n项和,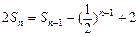 ,
,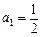
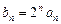 ,证明:数列
,证明:数列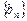 是等差数列;
是等差数列;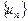 ,若存在常数M>0,对任意的
,若存在常数M>0,对任意的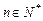 ,恒有
,恒有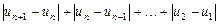 ≤M成立,称数列
≤M成立,称数列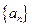 的前
的前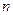 项和为
项和为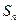 ,对任意的正整数
,对任意的正整数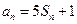 成立,记
成立,记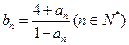 。
。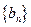 的通项公式;
的通项公式;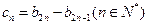 ,设数列
,设数列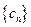 的前
的前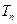 ,求证:对任意正整数
,求证:对任意正整数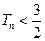 ;
;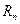 。已知正实数
。已知正实数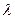 满足:对任意正整数
满足:对任意正整数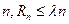 恒成立,求
恒成立,求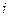 行共有
行共有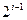 个正整数.设
个正整数.设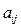 (i、j∈N*)表示位于这个数表中从上往下数第i行,从左往右数第j个数.
(i、j∈N*)表示位于这个数表中从上往下数第i行,从左往右数第j个数. 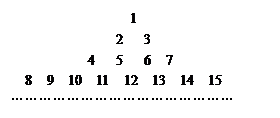
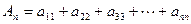
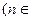 N*),试比较
N*),试比较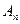 与
与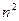
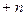 的大小,并说明理由.
的大小,并说明理由.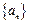 的前
的前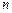 项和
项和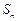 满足
满足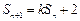 ,且
,且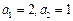

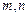 ,使
,使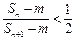 成立?若存在,求出这样的正整数;若不存在,说明理由.
成立?若存在,求出这样的正整数;若不存在,说明理由. 和正项等比数列
和正项等比数列 ,a7是b3和b7的等比中项.
,a7是b3和b7的等比中项. 的通项公式;
的通项公式; ,求数列{
,求数列{ }的前n项和Tn.
}的前n项和Tn. }的前11项和为 ()
}的前11项和为 ()