题目内容
已知数列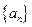 满足
满足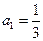 ,
, ,
,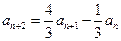
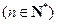 .
.
⑴求数列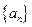 的通项公式;
的通项公式;
⑵求数列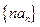 的前
的前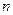 项和
项和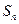 ;
;
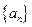 满足
满足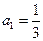 ,
, ,
,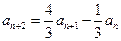
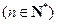 .
.⑴求数列
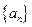 的通项公式;
的通项公式;⑵求数列
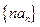 的前
的前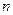 项和
项和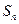 ;
; ⑴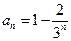
⑵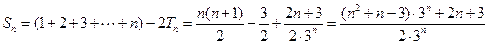
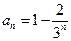
⑵
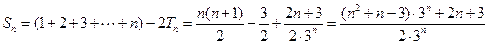
⑴方法一:由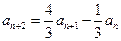 ,得
,得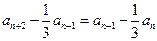 ,
,
∴数列 是常数列,
是常数列,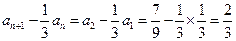 ,
,
即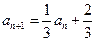 ,得
,得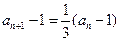 .
.
∴数列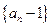 是首项为
是首项为 ,公比为
,公比为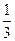 的等比数列,
的等比数列,
∴ ,故数列
,故数列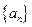 的通项公式为
的通项公式为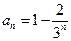 . …………7分
. …………7分
方法二:由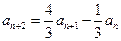 ,得
,得 ,
,
∴数列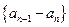 是首项为
是首项为 ,公比为
,公比为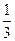 的等比数列,
的等比数列,
∴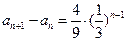 .
.
∴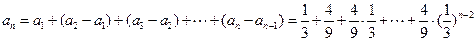
 (*)
(*)
当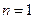 时,
时,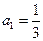 也适合(*),故数列
也适合(*),故数列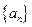 的通项公式为
的通项公式为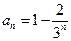 . …………7分
. …………7分
方法三:由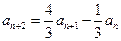 ,得
,得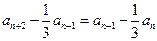 ,
, .
.
∴ 是常数列,
是常数列,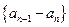 是首项为
是首项为 ,公比为
,公比为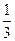 的等比数列.
的等比数列.
∴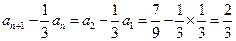 ,且
,且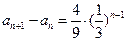 .
.
由上式联立消去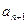 ,解得:
,解得: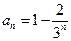 为数列
为数列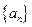 的通项公式. ………7分
的通项公式. ………7分
⑵解: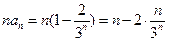 .
.
设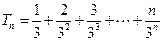 , ① 则
, ① 则 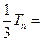
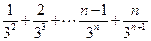 . ②
. ②
①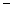 ②得:
②得: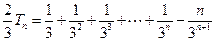
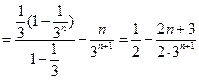 ,
,
∴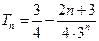 .
.
故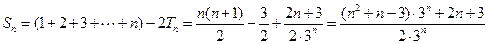 .……14分
.……14分
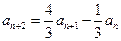 ,得
,得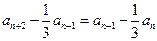 ,
, ∴数列
 是常数列,
是常数列,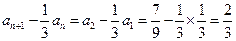 ,
,即
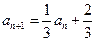 ,得
,得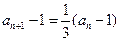 .
.∴数列
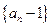 是首项为
是首项为 ,公比为
,公比为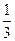 的等比数列,
的等比数列,∴
 ,故数列
,故数列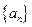 的通项公式为
的通项公式为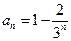 . …………7分
. …………7分方法二:由
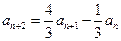 ,得
,得 ,
,∴数列
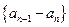 是首项为
是首项为 ,公比为
,公比为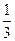 的等比数列,
的等比数列,∴
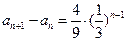 .
.∴
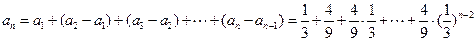
 (*)
(*)当
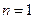 时,
时,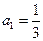 也适合(*),故数列
也适合(*),故数列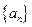 的通项公式为
的通项公式为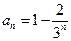 . …………7分
. …………7分方法三:由
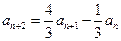 ,得
,得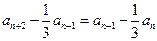 ,
, .
.∴
 是常数列,
是常数列,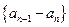 是首项为
是首项为 ,公比为
,公比为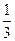 的等比数列.
的等比数列.∴
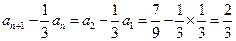 ,且
,且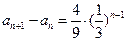 .
. 由上式联立消去
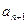 ,解得:
,解得: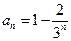 为数列
为数列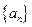 的通项公式. ………7分
的通项公式. ………7分⑵解:
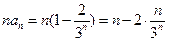 .
.设
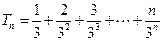 , ① 则
, ① 则 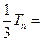
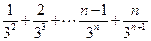 . ②
. ② ①
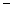 ②得:
②得: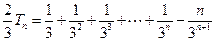
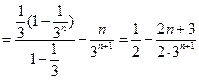 ,
,∴
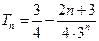 .
. 故
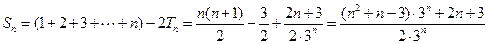 .……14分
.……14分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (n∈N*),求
(n∈N*),求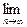 (b1+b2+b3+…+bn-n).
(b1+b2+b3+…+bn-n).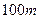 ,降低
,降低 ℃,已知山顶处的温度是
℃,已知山顶处的温度是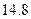 ℃,山脚处的温度为
℃,山脚处的温度为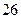 ℃,问此山相对于山脚处的高度是多少米.
℃,问此山相对于山脚处的高度是多少米. 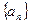 中,
中,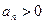 ,其公差
,其公差 ;数列
;数列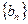 是等比数列,
是等比数列, ,其公比
,其公比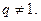
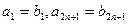 ,试比较
,试比较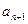 与
与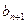 的大小,说明理由;
的大小,说明理由; ,试比较
,试比较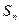 为等差数列
为等差数列 的前
的前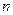 项和,
项和,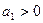 ,
,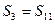 ,问数列的前几项和最大?
,问数列的前几项和最大? ,
,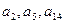 成等比数列,求数列
成等比数列,求数列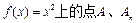 的横坐标分别为1和
的横坐标分别为1和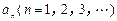 ,且a1=5,数列{xn}满足xn+1 = tf (xn – 1) + 1(t > 0且
,且a1=5,数列{xn}满足xn+1 = tf (xn – 1) + 1(t > 0且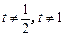 ).设区间
).设区间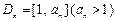 ,当
,当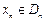 时,曲线C上存在点
时,曲线C上存在点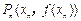 使得xn的值与直线AAn的斜率之半相等.
使得xn的值与直线AAn的斜率之半相等.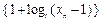 是等比数列;
是等比数列;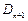
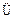
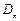 对一切
对一切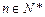 恒成立时,求t的取值范围;
恒成立时,求t的取值范围;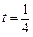 时,试比较Sn与n + 7的大小,并证明你的结论.
时,试比较Sn与n + 7的大小,并证明你的结论.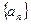 中,
中,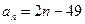 ,当数列
,当数列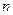 项和
项和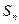 取得最小值时,
取得最小值时,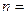 .
. 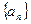 中,若
中,若 ,则
,则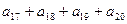 的值为( )
的值为( )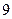


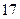
 、
、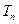 分别是等差数列
分别是等差数列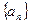 、
、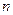 项和,
项和, ,则
,则 .
.