题目内容
15.已知函数f(x)=ex+x2(x<0),g(x)=x2-4x+$\frac{9}{2}$+ln(x+t-2),若f(x)的图象上存在一点P,它关于直线x=1的对称点P′落在y=g(x)的图象上,则t的取值范围是( )| A. | (-∞,$\frac{1}{\sqrt{e}}$) | B. | (-$\sqrt{e}$,$\frac{1}{\sqrt{e}}$) | C. | (-$\frac{1}{\sqrt{e}}$,$\sqrt{e}$) | D. | (0,$\sqrt{e}$) |
分析 由题意可得ex0-$\frac{1}{2}$-8x0-ln(t-x0)=0有负根,函数函数h(x)=ex-8x-$\frac{1}{2}$-ln(t-x)为增函数,由此能求出t的取值范围.
解答 解:f(x)的图象上存在一点P(x,y),关于直线x=1的对称点P′(2-x,y),
∴ex+x2=(x-2)2-4(2-x)+$\frac{9}{2}$+ln(2-x+t-2)=(x-2)2-4(2-x)+$\frac{9}{2}$+ln(t-x),
即ex-8x-$\frac{1}{2}$-ln(t-x)=0,
存在x0∈(-∞,0),即ex0-$\frac{1}{2}$-8x0-ln(t-x0)=0有负根,
∵当x趋近于负无穷大时,ex0-$\frac{1}{2}$8x0-ln(t-x0)也趋近于负无穷大,
∴函数h(x)=ex-8x-$\frac{1}{2}$-ln(t-x)为增函数,
∴h(0)=$\frac{1}{2}$-lnt>0,
∴lnt<ln$\sqrt{e}$,
∴0<t<$\sqrt{e}$
故选:D.
点评 本题考查的知识点是函数的图象和性质,函数的零点,函数单调性的性质,函数的极限,是函数图象和性质较为综合的应用,难度大.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
6.已知sinα+cos(π-α)=$\frac{1}{3}$,则sin2α的值为( )
| A. | $\frac{8}{9}$ | B. | $\frac{1}{9}$ | C. | $-\frac{8}{9}$ | D. | $\frac{4}{9}$ |
10.已知数列{an}满足2an+1+an=0,a2=1,则{an}的前9项和等于( )
| A. | -$\frac{2}{3}$(1-2-9) | B. | $\frac{1}{3}$(1-2-9) | C. | -$\frac{4}{3}$(1+2-9) | D. | (1-2-9) |
7.在某学校组织的一次利于定点投篮训练中,规定每人最多投3次;在A处每投进一球得3分,在B处每投进一球得2分;如果前两次得分之和超过3分即停止投篮,否则投第三次.某同学在A处的命中率q1为$\frac{1}{4}$,在B处的命中率为q2.该同学选择先在A处投一球,以后都在B处投,用ξ表示该同学投篮训练结束后所得的总分,其分布列为:
(I)求q2的值;
(Ⅱ)求随机变量ξ的数学期望.
| ξ | 0 | 2 | 3 | 4 | 5 |
| P | $\frac{3}{25}$ | p1 | p2 | p3 | p4 |
(Ⅱ)求随机变量ξ的数学期望.
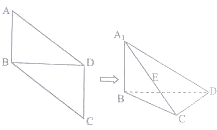 如图,在平行四边形ABCD中,AB=1,BD=$\sqrt{2}$,∠ABD=90°,将△ABD沿对角线BD折起,折后的点A变为A1,且A1C=2.
如图,在平行四边形ABCD中,AB=1,BD=$\sqrt{2}$,∠ABD=90°,将△ABD沿对角线BD折起,折后的点A变为A1,且A1C=2.