题目内容
13.已知tan2θ=-2$\sqrt{2}$,且π<2θ<2π,求$\frac{2co{s}^{2}\frac{θ}{2}-sinθ-1}{\sqrt{2}sin(θ+\frac{π}{2})}$的值.分析 利用二倍角的正切函数,求出正切函数值,利用二倍角的余弦函数以及诱导公式化简所求表达式,然后求解即可.
解答 解:tan2θ=-2$\sqrt{2}$,且π<2θ<2π,∴θ∈($\frac{π}{2},π$)
可得$\frac{2tanθ}{1-{tan}^{2}θ}=-2\sqrt{2}$,
解得tan$θ=\sqrt{2}$(舍去)或tanθ=$-\frac{\sqrt{2}}{2}$
$\frac{2co{s}^{2}\frac{θ}{2}-sinθ-1}{\sqrt{2}sin(θ+\frac{π}{2})}$=$\frac{cosθ-sinθ}{\sqrt{2}cosθ}$=$\frac{1-tanθ}{\sqrt{2}}$=$\frac{\sqrt{2}+1}{2}$.
点评 本题考查二倍角公式的应用,三角函数化简求值,考查计算能力.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
8.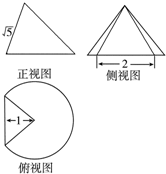 一个圆锥被过顶点的平面截去了较小的一部分,余下的几何体的三视图如图,则该几何体的表面积为( )
一个圆锥被过顶点的平面截去了较小的一部分,余下的几何体的三视图如图,则该几何体的表面积为( )
 一个圆锥被过顶点的平面截去了较小的一部分,余下的几何体的三视图如图,则该几何体的表面积为( )
一个圆锥被过顶点的平面截去了较小的一部分,余下的几何体的三视图如图,则该几何体的表面积为( )| A. | $\sqrt{5}$+$\frac{3\sqrt{3}π}{2}$+$\frac{3π}{2}$+1 | B. | 2$\sqrt{5}$+3$\sqrt{3}$π+$\frac{3π}{2}$+1 | C. | $\sqrt{5}$+$\frac{3\sqrt{3}π}{2}$+$\frac{3π}{2}$ | D. | $\sqrt{5}$+$\frac{3\sqrt{3}π}{2}$+$\frac{π}{2}$+1 |
2.若$\frac{π}{2}$<α<π,化简$\sqrt{\frac{1+sinα}{1-sinα}}-\sqrt{\frac{1-sinα}{1+sinα}}$的结果是( )
| A. | -2tanα | B. | 2tanα | C. | -2cotα | D. | 2cotα |