题目内容
3.已知等差数列{an}的首项a1=1,公差d>0,前n项和Sn(1)若S1,S2,S4成等比数列,求数列$\left\{{\frac{a_n}{2^n}}\right\}$的前n项和Tn;
(2)若$\frac{1}{{{a_1}{a_2}}}+\frac{1}{{{a_2}{a_3}}}+\frac{1}{{{a_3}{a_4}}}+…+\frac{1}{{{a_n}{a_{n+1}}}}$>$\frac{2015}{2016}$对一切n∈N*恒成立,求d的取值范围.
分析 (1)由S1=1,S2=2+d,S4=4+6d可得(2+d)2=4+6d;从而解得d=2;化简$\frac{a_n}{2^n}$=$\frac{2n-1}{2^n}$,从而求前n项和;
(2)化简$\frac{1}{{{a_1}{a_2}}}+\frac{1}{{{a_2}{a_3}}}+\frac{1}{{{a_3}{a_4}}}+…+\frac{1}{{{a_n}{a_{n+1}}}}$=$\frac{1}{d}[(\frac{1}{a_1}-\frac{1}{a_2})+(\frac{1}{a_2}-\frac{1}{a_3})+…+(\frac{1}{a_n}-\frac{1}{{{a_{n-1}}}})]$=$\frac{n}{1+nd}$;从而可得d<$\frac{2016}{2015}-\frac{1}{n}$对一切n∈N*恒成立,从而解得.
解答 解:(1)∵S1=1,S2=2+d,S4=4+6d,
∴(2+d)2=4+6d;
解得d=2或d=0(舍去);
∴an=2n-1,
∴$\frac{a_n}{2^n}$=$\frac{2n-1}{2^n}$,
∴Tn=$\frac{1}{2}+\frac{3}{2^2}+\frac{5}{2^3}+…+\frac{2n-1}{2^n}$,
∴$\frac{1}{2}$Tn=$\frac{1}{2^2}+\frac{3}{2^3}+…+\frac{2n-3}{2^n}+\frac{2n-1}{{{2^{n+1}}}}$,
∴$\frac{1}{2}$Tn=$\frac{1}{2}+2(\frac{1}{2^2}+\frac{1}{2^3}+…+\frac{1}{2^n})-\frac{2n-1}{{{2^{n+1}}}}=\frac{3}{2}-\frac{2n+3}{{{2^{n+1}}}}$;
∴Tn=$3-\frac{2n+3}{2^n}$.
(2)∵$\frac{1}{{{a_1}{a_2}}}+\frac{1}{{{a_2}{a_3}}}+\frac{1}{{{a_3}{a_4}}}+…+\frac{1}{{{a_n}{a_{n+1}}}}$
=$\frac{1}{d}[(\frac{1}{a_1}-\frac{1}{a_2})+(\frac{1}{a_2}-\frac{1}{a_3})+…+(\frac{1}{a_n}-\frac{1}{{{a_{n-1}}}})]$
=$\frac{n}{1+nd}$;
∴$\frac{n}{1+nd}$>$\frac{2015}{2016}$对一切n∈N*恒成立,
∴d<$\frac{2016}{2015}-\frac{1}{n}$对一切n∈N*恒成立,
∴0<d<$\frac{1}{2015}$.
点评 本题考查了等差数列与等比数列的性质应用及数列前n项和的求法,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 最大值为3,无最小值 | B. | 无最大值,最小值为3 | ||
| C. | 无最大值,无最小值 | D. | 无最大值,最小值为$\frac{33}{2}$ |
| A. | $\frac{{S}_{8}}{{a}_{8}}$ | B. | $\frac{{S}_{9}}{{a}_{9}}$ | C. | $\frac{{S}_{10}}{{a}_{10}}$ | D. | $\frac{{S}_{11}}{{a}_{11}}$ |
| A. | 2b<2a<2 | B. | $0<{log_{\frac{1}{2}}}a<{log_{\frac{1}{2}}}$b | ||
| C. | ab<b2<1 | D. | ab<a2<1 |
| A. | (-2,4) | B. | (-4,2) | C. | (-1,3) | D. | (-3,1) |
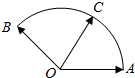 给定两个长度为1的平面向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°.点C在以OA,OB为半径的圆弧上,∠AOC=30°如图所示,若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x=$\frac{2\sqrt{3}}{3}$;y=$\frac{\sqrt{3}}{3}$.
给定两个长度为1的平面向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°.点C在以OA,OB为半径的圆弧上,∠AOC=30°如图所示,若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x=$\frac{2\sqrt{3}}{3}$;y=$\frac{\sqrt{3}}{3}$.