题目内容
2．已知a，b为正整数，且a+b=1，求证：$\frac{1}{a}$+$\frac{1}{b}$≥4．分析 由题意可得$\frac{1}{a}$+$\frac{1}{b}$=（$\frac{1}{a}$+$\frac{1}{b}$）（a+b）=2+$\frac{b}{a}$+$\frac{a}{b}$，由基本不等式可得．
解答 证明：∵a，b为正整数，且a+b=1，
∴$\frac{1}{a}$+$\frac{1}{b}$=（$\frac{1}{a}$+$\frac{1}{b}$）（a+b）
=2+$\frac{b}{a}$+$\frac{a}{b}$≥2+2$\sqrt{\frac{b}{a}•\frac{a}{b}}$=4，
当且仅当$\frac{b}{a}$=$\frac{a}{b}$即a=b=$\frac{1}{2}$时取等号．
点评 本题考查不等式的证明，涉及基本不等式求最值问题，属基础题．
练习册系列答案
相关题目
12．已知f（x）、g（x）、h（x）均为一次函数．若对实数x满足：
|f（x）|-|g（x）|+h（x）=$\left\{\begin{array}{l}{-2，x＜-1}\\{7x+5，-1≤x＜0}\\{-4x+5，x≥0}\end{array}\right.$，h（x）的解析式为．
|f（x）|-|g（x）|+h（x）=$\left\{\begin{array}{l}{-2，x＜-1}\\{7x+5，-1≤x＜0}\\{-4x+5，x≥0}\end{array}\right.$，h（x）的解析式为．
| A． | 2x-$\frac{3}{2}$ | B． | -2x-$\frac{3}{2}$ | C． | 2x+$\frac{3}{2}$ | D． | -2x+$\frac{3}{2}$ |
10．若sin（π+α）+cos（$\frac{π}{2}$+α）=-m，则cos（$\frac{3}{2}π$-α）+2sin（2π-α）的值为（ ）
| A． | -$\frac{2m}{3}$ | B． | $\frac{2m}{3}$ | C． | -$\frac{3m}{2}$ | D． | $\frac{3m}{2}$ |
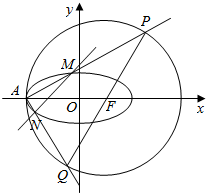已知A（-2，0）是椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）与圆F：（x-c）2+y2=9的一个交点，且圆心F是椭圆的一个焦点，