题目内容
8.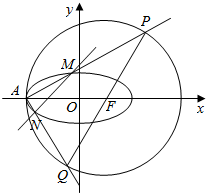 已知A(-2,0)是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)与圆F:(x-c)2+y2=9的一个交点,且圆心F是椭圆的一个焦点,
已知A(-2,0)是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)与圆F:(x-c)2+y2=9的一个交点,且圆心F是椭圆的一个焦点,(1)求椭圆C的方程;
(2)过F的直线交圆与P、Q两点,连AP、AQ分别交椭圆与M、N点,试问直线MN是否过定点?若过定点,则求出定点坐标;若不过定点,请说明理由.
分析 (1)把A(-2,0)代入圆F:(x-c)2+y2=9的方程,可得(-2-c)2=9,c>0,解得c.可得F(1,0),A(-2,0)为椭圆的一个顶点,可得a.即可得出椭圆的标准方程.
(2)由∠PAQ所对的弦是直径PQ.设直线AP的方程为:y=k(x+2),同理可得直线AQ的方程为:y=-$\frac{1}{k}$(x+2).分别与椭圆方程联立可得:xM,yM.xN,yN.直线MN的方程为:y-yM=$\frac{{y}_{M}-{y}_{N}}{{x}_{M}-{x}_{N}}$(x-xM),令y=0,则x=$\frac{{y}_{M}{x}_{N}-{y}_{N}{x}_{M}}{{y}_{M}-{y}_{N}}$,即可得出.
解答 解:(1)把A(-2,0)代入圆F:(x-c)2+y2=9的方程,可得(-2-c)2=9,c>0,解得c=1.
可得F(1,0),
A(-2,0)为椭圆的一个顶点,∴a=2.
∴b2=a2-c2=3.
∴椭圆C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1.
(2)∵∠PAQ所对的弦是直径PQ.
设直线AP的方程为:y=k(x+2),
同理可得直线AQ的方程为:y=-$\frac{1}{k}$(x+2).
联立$\left\{\begin{array}{l}{y=k(x+2)}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,化为:(3+4k2)x2+16k2x+16k2-12=0,
-2+xM=$\frac{-16{k}^{2}}{3+4{k}^{2}}$,解得xM=$\frac{6-8{k}^{2}}{3+4{k}^{2}}$,yM=k(xM+2)=$\frac{12k}{3+4{k}^{2}}$.
同理可得:xN=$\frac{6{k}^{2}-8}{3{k}^{2}+4}$,yN=$-\frac{1}{k}$(xN+2)=-$\frac{12k}{3{k}^{2}+4}$.
直线MN的方程为:y-yM=$\frac{{y}_{M}-{y}_{N}}{{x}_{M}-{x}_{N}}$(x-xM),
令y=0,则x=$\frac{{y}_{M}{x}_{N}-{y}_{N}{x}_{M}}{{y}_{M}-{y}_{N}}$=$-\frac{2}{7}$.
因此可得:直线MN过定点$(-\frac{2}{7},0)$.
点评 本题考查了椭圆与圆的标准方程及其性质、直线与椭圆相交弦长问题、直线过定点问题、相互垂直的直线斜率之间的关系,考查了推理能力与计算能力,属于难题.

| A. | 9 | B. | 16 | C. | 20 | D. | 25 |
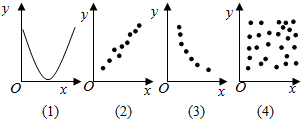 如图,两个变量具有相关关系的图是( )
如图,两个变量具有相关关系的图是( )| A. | (1)(2) | B. | (1)(3) | C. | (2)(4) | D. | (2)(3) |