题目内容
一空间几何体的三视图如图所示,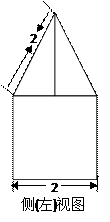
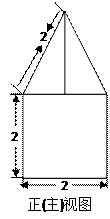
求该几何体的体积。
该空间几何体为一圆柱和一四棱锥组成的,圆柱的底面半径为1,高为2,体积为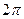
,四棱锥的底面边长为
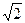，高为
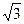，所以体积为
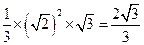所以该几何体的体积为
.
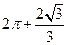解析
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
黄冈小状元解决问题天天练系列答案三点一测快乐周计划系列答案题目内容
一空间几何体的三视图如图所示,
求该几何体的体积。
该空间几何体为一圆柱和一四棱锥组成的,圆柱的底面半径为1,高为2,体积为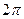,四棱锥的底面边长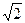为，高为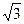，所以体积为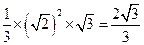所以该几何体的体积为.
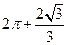解析
黄冈小状元解决问题天天练系列答案三点一测快乐周计划系列答案
的侧棱与底面垂直，
，
，
，
分别是
，
的中点，点
在直线
上，且
；
取何值，总有
；
与平面
所成的角
最大？并求该角取最大值时的正切值；
与平面
的三视图如图所示,
平面
;
平面
;
中，E、F、G分别为
、
、
的中点，O为
与
的交点，
面
与平面
cm，面积为
cm2的扇形铁皮制作一个无盖的圆锥形容器（衔接部分忽略不计）， 该容器最多盛水多少？（结果精确到0.1 cm3）
的边长为1，分别取边
的中点
，连结
， 
重合于一点
，得到一 
；
。 
（1）求证:
；（2）是否在线段
上存在一
点,使二面角
的平
，设
，若存在，求
；若不存在，说明理由
，求这个正三棱锥的侧面积