题目内容
(本小题满分12分)
如图6,已知正三棱柱ABC—A1B1C1中,D是BC的中点,AA1=AB=1。
(1)求证:平面AB1D⊥平面B1BCC1;
(2)求证:A1C//平面AB1D;
(3)求二面角B—AB1—D的正切值。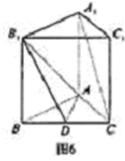
(1)证明见解析。
(2)证明见解析。
(3)二面角B—AB1—D的正切值为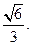
解析解法一:
证明:( 1)因为B1B⊥平面ABC,AD
1)因为B1B⊥平面ABC,AD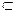 平面ABC,
平面ABC,
所以AD⊥B1B (1分)
因为D为正△ABC中BC的中点,[来源:学。科。网]
所以AD⊥BD (2分)
又B1B∩BC=B,
所以AD⊥平面B1BCC1 (3分)
又AD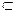 平面AB1D,故平面AB1D⊥平面B1BCC1 (4分)
平面AB1D,故平面AB1D⊥平面B1BCC1 (4分)
(2)连接A1B,交AB1于E,连DE (5分)
因为点E为矩形A1ABB1对角线的交点,所以E为AB1的中点 (6分)
又D为BC 的中点,所以DE为△A1BC的中位线,
的中点,所以DE为△A1BC的中位线,
所以DE//A1C (7分)
又DE 平面AB1D,所以A1C//平面AB1D (8分)
平面AB1D,所以A1C//平面AB1D (8分)
(3)解:过D作DF⊥AB于F,过F作FG⊥AB1于G,连接DG。
因为平面A1ABB1⊥平面ABC,DF⊥AB,所以DF⊥平面A1ABB1。
又AB1 平面A1ABB1,所以AB1⊥DF。
平面A1ABB1,所以AB1⊥DF。
又FG⊥AB1,所以AB1⊥平面DFG,所以AB1⊥DG。 (9分)
又AB1⊥FG,所以∠DGF为 二面角B—AB1—D的平面角。 (10分)
二面角B—AB1—D的平面角。 (10分)
因为AA1=AB=1,
所以在正△ABC中,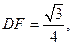 [来源:学+科+网]
[来源:学+科+网]
在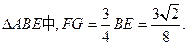 (11分)
(11分)
所以在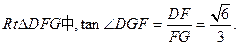 (12分)
(12分)
解法二:
解:建立如图所示的直角坐标系,依题意有: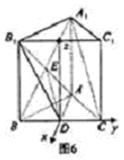

(1)证明:由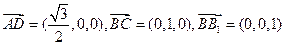 ,
,
得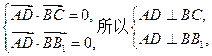
又BC∩⊥BB1=B,所以AD⊥平面B1BCC1。 (4分)
又AD 平面AB1D,所以平面AB1D⊥B1BCC1 (5分)
平面AB1D,所以平面AB1D⊥B1BCC1 (5分)
(2)证明:连接A1B,交AB1于E,连DE,
因为点E为正方形A1ABB1对角线的交点,所以E为AB1的中点,
即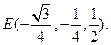 (6分)
(6分)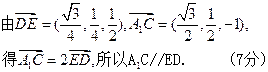
又DE 平面AB1D,所以A1C//平面AB1D (8分)[来源:Z+xx+k.Com]
平面AB1D,所以A1C//平面AB1D (8分)[来源:Z+xx+k.Com]
(3)解:设平面ABB1的一个法向量为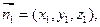
由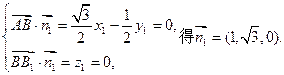 (9分)
(9分)
设平面AB1D的一个法向量为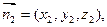
由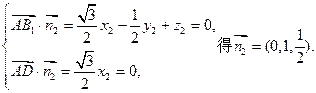 (10分)
(10分)
所以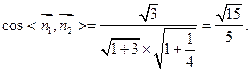 (11分)
(11分)
所以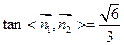 ,
,
依图可得二面角B—AB1—D的正切值为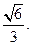 (12分)
(12分)

 名校课堂系列答案
名校课堂系列答案过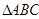 所在平面
所在平面 外一点
外一点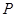 ,作
,作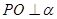 ,垂足为
,垂足为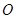 ,连接
,连接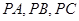 .若
.若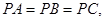 则点
则点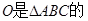 ( )
( )
| A.垂心 | B.外心 | C.内心 | D.重心 |
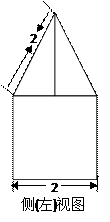
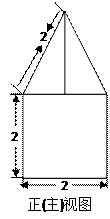
 为正三角形,EC
为正三角形,EC
 平面ABC,BD
平面ABC,BD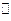 CE,且CE=CA=2BD=a,M是EA的中点.(1)求证:(1) DM
CE,且CE=CA=2BD=a,M是EA的中点.(1)求证:(1) DM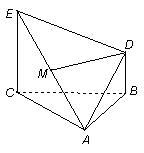
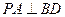 ;
;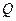 为
为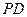 上一点,且
上一点,且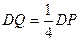 ,求二面角
,求二面角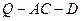 的大小.
的大小.
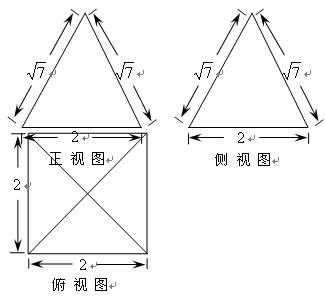
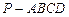 中,底面
中,底面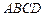 是一直角梯形,
是一直角梯形,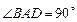 ,
,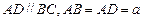 ,
,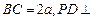 底面
底面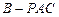 的体积;
的体积;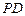 上是否存在一点
上是否存在一点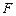 ,使得
,使得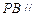 平面
平面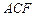 ,若存在,求出
,若存在,求出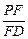 的值;若不存在,试说明理由.
的值;若不存在,试说明理由.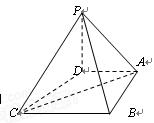
 本题满分12分)
本题满分12分)