题目内容
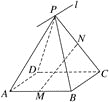
【题目】如图,在底面为正方形的四棱锥P-ABCD中,侧棱PD⊥底面ABCD,PD=DC,点E是线段PC的中点.

(1)求异面直线AP与BE所成角的大小;
(2)若点F在线段PB上,使得二面角F-DE-B的正弦值为![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
试题分析:由已知条件可得两两垂直,因此以它们为坐标轴建立空间直角坐标系,设![]() ,写出各点坐标,(2)求得
,写出各点坐标,(2)求得![]() 的夹角可得异面直线AP与BE所成角的大小(这个角是锐角);(2)
的夹角可得异面直线AP与BE所成角的大小(这个角是锐角);(2)![]() ,再求出
,再求出![]() 的坐标,然后求出平面
的坐标,然后求出平面![]() 和平面
和平面![]() 的法向量,则法向量夹角与二面角相等或互补,可得出
的法向量,则法向量夹角与二面角相等或互补,可得出![]() 的方程,解之可得
的方程,解之可得![]() 值.
值.
试题解析:(1)在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PD⊥底面ABCD,所以DA、DC、DP两两垂直,故以![]() 为正交基底,建立空间直角坐标系D-xyz.
为正交基底,建立空间直角坐标系D-xyz.

因为PD=DC,所以DA=DC=DP,不妨设DA=DC=DP=2,
则D(0,0,0),A(2,0,0),C(0,2,0),P(0,0,2),B(2,2,0).
因为E是PC的中点,所以E(0,1,1).
所以![]() =(-2,0,2),
=(-2,0,2),![]() =(-2,-1,1),
=(-2,-1,1),
所以cos<![]() ,
,![]() >=
>=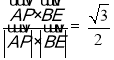 ,
,
从而<![]() ,
,![]() >=
>=![]()
因此异面直线AP与BE所成角的大小为![]() .
.
(2)由(1)可知,![]() =(0,1,1),
=(0,1,1),![]() =(2,2,0),
=(2,2,0),![]() =(2,2,-2).
=(2,2,-2).
设![]() =λ
=λ![]() ,则
,则![]() =(2λ,2λ,-2λ),从而
=(2λ,2λ,-2λ),从而![]() =
=![]() +
+![]() =(2λ,2λ,2-2λ).
=(2λ,2λ,2-2λ).
设m=(x1,y1,z1)为平面DEF的一个法向量,
则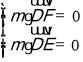 即
即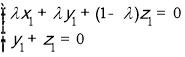
取z1=λ,则y1=-λ,x1=2λ-1.
所以m=(2λ-1,-λ,λ)为平面DEF的一个法向量.
设n=(x2,y2,z2)为平面DEB的一个法向量,
则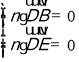 即
即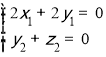
取x2=1,则y2=-1,z2=1.
所以n=(1,-1,1)为平面BDE的一个法向量.
因为二面角F-DE-B的正弦值为![]() ,所以二面角F-DE-B的余弦的绝对值为
,所以二面角F-DE-B的余弦的绝对值为![]() ,
,
即|cos<m,n>|=![]() ,
,
所以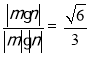 ,
,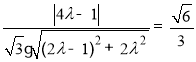 ,
,
化简得,4λ2=1,因为点F在线段PB上,所以0≤λ≤1,所以λ=![]() ,即
,即![]() .
.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案