Question

【题目】在0~1之间随机选择两个数,这两个数对应的点将长度为1的线段分成三条,试求这三条线段能构成三角形的概率.

Answer 1

【答案】

【解析】试题分析：先设线段其中两段的长度分别为x、y，分别表示出线段随机地折成3段的x，y的约束条件和3段构成三角形的约束条件，再画出约束条件表示的平面区域，利用面积测度即可求出构成三角形的概率．

解析:设三条线段的长度分别为x,y,1-x-y,

则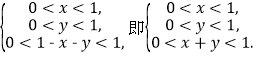

在平面上建立如图所示的直角坐标系,围成三角形区域G,每对(x,y)对应着G内的点(x,y),由题意知,每一个试验结果出现的可能性相等,因此,试验属于几何概型.

记事件A={三条线段能构成三角形},则事件A发生当且仅当因此图中的阴影区域g就表示“三条线段能构成三角形”,即事件A发生.容易求得g的面积为,G的面积为,

则P(A)=.