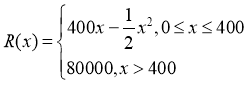题目内容
【题目】已知函数![]() .
.
(1)试讨论函数![]() 的单调性;
的单调性;
(2)证明:![]() .
.
【答案】(1)![]() 时,
时,![]() 在
在![]() 上递减,
上递减,![]() 时,
时,![]() 时递减,
时递减,![]() 时递增;(2)证明见解析.
时递增;(2)证明见解析.
【解析】
试题分析:(1)判断单调性,定义域为![]() ,只要求得导数
,只要求得导数![]() ,判断
,判断![]() 的正负即可,此题需要按
的正负即可,此题需要按![]()
![]() 和
和![]() 分类讨论;(2)证明此不等式的关键是求
分类讨论;(2)证明此不等式的关键是求![]() 的最大值,由导数的知识可得
的最大值,由导数的知识可得![]() 最大值为
最大值为![]() ,即
,即![]() ,当
,当![]() 时,
时,![]() .从而
.从而![]() ,这样要证不等式的左边每一项都可以放大:
,这样要证不等式的左边每一项都可以放大:![]()
![]() ,并且再放大为
,并且再放大为![]() ,求和后,不等式右边用裂项相消法可得.
,求和后,不等式右边用裂项相消法可得.
试题解析:(1)由题可知![]() ,
,
定义域为![]() ,
,
所以![]() ,
,
若![]() ,
,![]() 恒成立,
恒成立,![]() 在
在![]() 单调递减.
单调递减.
若![]() ,
,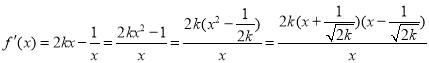 ,
,
当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
(2)令![]() ,则
,则![]() ,
,
设![]() ,由于
,由于![]() ,令
,令![]() 得
得![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,
,![]() 单调递减
单调递减
所以![]() ,
,
所以当![]() 时,
时,![]() 对
对![]() 恒成立,即
恒成立,即![]() ,
,
从而![]() ,
,
从而得到![]() ,对
,对![]() 依次取值
依次取值![]() 可得
可得
![]()
![]()
![]() …,
…,![]() ,
,
对上述不等式两边依次相加得到:
![]() ,
,
又因为![]() ,
,
而![]()
![]() ,
,
所以![]() ,
,
所以![]()

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目