题目内容
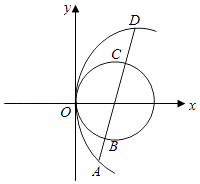
【题目】在平面直角坐标系中，圆O：x2+y2=4与x轴的正半轴交于点A，以A为圆心的圆A：（x﹣2）2+y2=r2（r＞0）与圆O交于B，C两点．
（1）若直线l与圆O切于第一象限，且与坐标轴交于D，E，当线段DE长最小时，求直线l的方程；
（2）设P是圆O上异于B，C的任意一点，直线PB、PC分别与x轴交于点M和N，问OMON是否为定值？若是，请求出该定值；若不是，请说明理由．
【答案】
（1）解：设直线l的方程为 
+ 
=1（a＞0，b＞0），
即bx+ay﹣ab=0，
由直线l与圆O相切得 
，
即 
，
，
（当且仅当 
时取等号），
此时直线l的方程为 
．
（2）设B（x0，y0），P（x1，y1）（y1≠±y0），
则C（x0，﹣y0）， 
， 
，
直线PB的方程为： 
，
直线PC的方程为： 
，
分别令y=0，得 
，
所以OMON= 
为定值．
【解析】（1）根据截距式设出直线方程l，根据直线与圆相切，圆心到直线的距离等于半径，可得到
，再表示出DE2应用均值不等式即可得出取得最小值时a，b的值，从而得到直线方程，（2）根据题意设设B（x0，y0），P（x1，y1）（y1≠±y0），则C（x0，﹣y0），表示出PB，PC的直线方程，求得xM，xN，从而代入可知OMON为定值.
练习册系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
