题目内容
【题目】在平面直角坐标系xOy中,已知椭圆C: ![]() (m>0)的离心率为
(m>0)的离心率为 ![]() ,A,B分别为椭圆的左、右顶点,F是其右焦点,P是椭圆C上异于A、B的动点.
,A,B分别为椭圆的左、右顶点,F是其右焦点,P是椭圆C上异于A、B的动点.
(1)求m的值及椭圆的准线方程;
(2)设过点B且与x轴的垂直的直线交AP于点D,当直线AP绕点A转动时,试判断以BD为直径的圆与直线PF的位置关系,并加以证明.
【答案】
(1)解:因为椭圆的离心率为 ![]() .所以
.所以 ![]() ,解得m=9.
,解得m=9.
所以椭圆的方程为 ![]()
准线方程为 ![]()
(2)解:由题可知A(﹣5,0),B(5,0),F(4,0),设P(x0,y0).
由椭圆的对称性,不妨设y0>0
①若x0=4,则 ![]() ,PF方程为x=4,AP方程为
,PF方程为x=4,AP方程为 ![]() ,D(5,2)
,D(5,2)
以BD为直径的圆的圆心(5,1),半径为1与直线PF相切;
②若x0≠4,则AP方程为 ![]()
令x=5,得 ![]() ,则
,则 ![]()
以BD为直径的圆的圆心 ![]() ,半径为
,半径为 ![]()
直线PF方程为 ![]() ,即y0x﹣(x0﹣4)y﹣4y0=0
,即y0x﹣(x0﹣4)y﹣4y0=0
圆心M到直线PF的距离 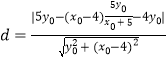
= 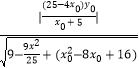 ═
═ 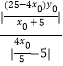 =
= ![]()
所以圆M与直线PF相切
综上所述,当直线AP绕点A转动时,以BD为直径的圆与直线PF相切
【解析】(1)根据题意由椭圆的离心率可求得m的值,进而得到椭圆的方程和准线方程。(2)讨论直线的斜率存在或不存在,设P(x0,y0)即得①若x0=4,直线PF的斜率不存在,由已知可得以BD为直径的圆的圆心(5,1),半径为1与直线PF相切。②若x0≠4,根据直线与圆相切的位置关系得证圆M与直线PF相切,进而得到直线AP绕点A转动时,以BD为直径的圆与直线PF相切。

练习册系列答案
相关题目