题目内容
【题目】设函数f(x)= ![]() ,a∈R,若存在实数b,使函数g(x)=f(x)﹣b有两个零点,则实数a的取值范围为 .
,a∈R,若存在实数b,使函数g(x)=f(x)﹣b有两个零点,则实数a的取值范围为 .
【答案】(﹣∞,﹣1)
【解析】解:∵g(x)=f(x)﹣b有两个零点
∴f(x)=b有两个零点,即y=f(x)与y=b的图象有两个交点,由于y=﹣x2在(﹣∞,a)递增,y=x3在[a,+∞)递增,要使y=f(x)与y=b的图象有两个交点,
可得 ![]() , 可得a<﹣1.
, 可得a<﹣1.
实数a的取值范围为:(﹣∞,﹣1).
所以答案是:(﹣∞,﹣1).
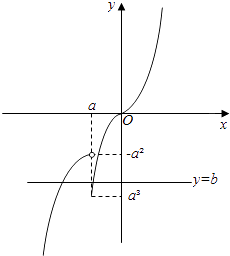
【考点精析】根据题目的已知条件,利用函数的图象的相关知识可以得到问题的答案,需要掌握函数的图像是由直角坐标系中的一系列点组成;图像上每一点坐标(x,y)代表了函数的一对对应值,他的横坐标x表示自变量的某个值,纵坐标y表示与它对应的函数值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目