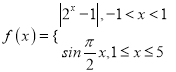题目内容
【题目】如右图抛物线顶点在原点，圆（x﹣2）2+y2=22的圆心恰是抛物线的焦点，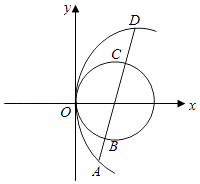
（Ⅰ）求抛物线的方程；
（Ⅱ）一直线的斜率等于2，且过抛物线焦点，它依次截抛物线和圆于A、B、C、D四点，求|AB|+|CD|的值．
【答案】解：（Ⅰ）设抛物线方程为y2=2px（p＞0），
∵圆（x﹣2）2+y2=22的圆心恰是抛物线的焦点，∴p=4．
∴抛物线的方程为：y2=8x；
（Ⅱ）依题意直线AB的方程为y=2x﹣4
设A（x1，y1），D（x2，y2），则 
，得x2﹣6x+4=0，
∴x1+x2=6，|AD|=x1+x2+p=6+4=10．
|AB|+|CD|=|AD|﹣|CB|=10﹣4=6．
【解析】（Ⅰ）本小题根据圆的方程确定圆的圆心，即确定抛物线的焦点坐标，进而求得抛物线的方程；（Ⅱ）本小题先根据所知条件求得直线AB的方程，再与抛物线方程联立求得以点A，点B横坐标为根的一元二次方程，再有抛物线上的点到焦点的距离与到准线的距离相等的特点得到：|AD|=x1+x2+p，最后由|AB|+|CD|=|AD|﹣|CB|求得|AB|+|CD|的值．
【考点精析】通过灵活运用圆的标准方程，掌握圆的标准方程：
；圆心为A(a,b),半径为r的圆的方程即可以解答此题．
练习册系列答案
考前必练系列答案
相关题目
