题目内容
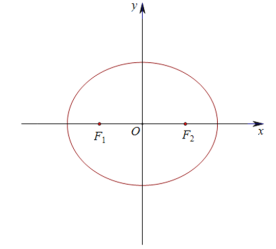
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点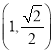 ,若点
,若点![]() 在椭圆C上,则点
在椭圆C上,则点![]() 称为点M的一个“椭点”.
称为点M的一个“椭点”.
(1)求椭圆C的标准方程;
(2)若直线![]() 与椭圆C相交于A,B两点,且A,B两点的“椭点”分别为P,Q,以PQ为直径的圆经过坐标原点,试判断
与椭圆C相交于A,B两点,且A,B两点的“椭点”分别为P,Q,以PQ为直径的圆经过坐标原点,试判断![]() 的面积是否为定值?若为定值,求出定值;若不为定值,说明理由.
的面积是否为定值?若为定值,求出定值;若不为定值,说明理由.
【答案】(1)![]() (2)为定值,
(2)为定值,![]()
【解析】
(1)根据椭圆![]() 的离心率为
的离心率为![]() ,得到
,得到![]() ,又过点
,又过点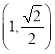 ,得到
,得到 ![]() ,联立求解.
,联立求解.
(2)设![]()
![]() ,则
,则![]()
![]() .联立直线
.联立直线![]() 与椭圆的方程,由于以
与椭圆的方程,由于以![]() 为直径的圆经过坐标原点,所以
为直径的圆经过坐标原点,所以![]() ,即
,即![]() 从而得到
从而得到![]() ,再求得弦长
,再求得弦长
![]() ,点o到直线的距离
,点o到直线的距离![]() ,得到
,得到![]() 再求解..
再求解..
(1)根据题意得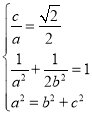 ,
,
解得![]()
所以椭圆的方程为![]() .
.
(2)设![]()
![]() ,则
,则![]()
![]() .
.
由于以![]() 为直径的圆经过坐标原点,所以
为直径的圆经过坐标原点,所以![]() ,即
,即![]() .
.
由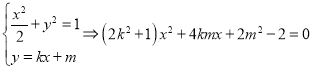 ,
, ![]() ,即
,即![]() ,
,
由韦达定理得 ![]()
![]() ,
, ![]() .
.
代入![]() ,得
,得![]() ,
,
![]() ,
,
原点到直线AB的距离为:![]() .
.
所以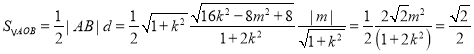
所以![]() 的面积为定值
的面积为定值![]() .
.

【题目】2019年6月13日,三届奥运亚军,羽坛传奇,马来西亚名将李宗伟宣布退役,当天有大量网友关注此事件,某网上论坛从关注此事件跟帖中,随机抽取了100名网友进行调查统计,先分别统计他们在跟帖中的留言条数,再把网友人数按留言条数分成6组;![]()
![]()
![]()
![]()
![]()
![]() ,得到如下图所小的频率分布直方图;并将其中留言不低于40条的规定为“强烈关注”,否则为“一般关注”,对这100名网友进一步统计,得到部分数据如下的列联表.
,得到如下图所小的频率分布直方图;并将其中留言不低于40条的规定为“强烈关注”,否则为“一般关注”,对这100名网友进一步统计,得到部分数据如下的列联表.
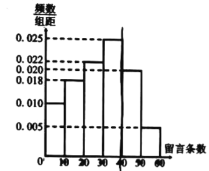

(1)在答题卡上补全2×2列联表中数据,并判断能否有95%的把握认为网友对此事件是否为“强烈关注”与性别有关?
(2)该论坛欲在上述“强烈关注”的网友中按性别进行分层抽样,共抽取5人,并在此5人中随机抽取两名接受访谈,记女性访谈者的人数为占,求5的分布列与数学期望.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式与数据: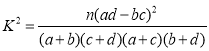 ,其中
,其中![]() .
.