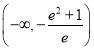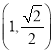题目内容
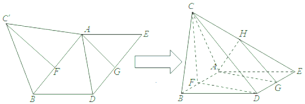
【题目】如图,一个正![]() 和一个平行四边形ABDE在同一个平面内,其中
和一个平行四边形ABDE在同一个平面内,其中![]() ,
,![]() ,AB,DE的中点分别为F,G.现沿直线AB将
,AB,DE的中点分别为F,G.现沿直线AB将![]() 翻折成
翻折成![]() ,使二面角
,使二面角![]() 为
为![]() ,设CE中点为H.
,设CE中点为H.
(1)(i)求证:平面![]() 平面AGH;
平面AGH;
(ii)求异面直线AB与CE所成角的正切值;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1) (i)证明见解析;(ii)![]() (2)
(2) ![]()
【解析】
(1)(i)通过证明四边形![]() 为平行四边形证得
为平行四边形证得![]() ;通过三角形中位线证得
;通过三角形中位线证得![]() ,由此证得平面
,由此证得平面![]() 平面AGH.
平面AGH.
(ii)根据![]() 和
和![]() 判断
判断![]() 是两个异面直线
是两个异面直线![]() 与
与![]() 所成角.用勾股定理求得
所成角.用勾股定理求得![]() ,利用余弦定理求得
,利用余弦定理求得![]() ,由此求得异面直线
,由此求得异面直线![]() 与
与![]() 所成角的正切值.
所成角的正切值.
(2)根据二面角的定义,判断出![]() 即为二面角
即为二面角![]() 的平面角,利用余弦定理求得二面角的余弦值.
的平面角,利用余弦定理求得二面角的余弦值.
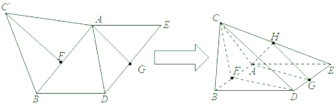
(1)(i)证明:连FD.因为ABDE为平行四边形,F、G分别为AB、DE中点,
所以FDGA为平行四边形,所以![]() .-
.-
又H、G分别为CE、DE的中点,所以![]() .
.
FD、![]() 平面AGH,AG、
平面AGH,AG、![]() 平面AGH,所以
平面AGH,所以![]() 平面AGH,
平面AGH,![]() 平面AGH,而FD、
平面AGH,而FD、![]() 平面CDF,所以平面
平面CDF,所以平面![]() 平面AGH.
平面AGH.
(ii)因为![]() ,所以
,所以![]() 或其补角即为异面直线AB与CE所成的角.
或其补角即为异面直线AB与CE所成的角.
因为ABC为正三角形,![]() ,F为AB中点,所以
,F为AB中点,所以![]() ,
,![]() ,从而
,从而![]() 平面CFD,而
平面CFD,而![]() ,所以
,所以![]() 平面CFD,因为
平面CFD,因为![]() 平面CFD,所以
平面CFD,所以![]() .-
.-
由条件易得![]() ,
,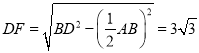 ,又
,又![]() 为二面角
为二面角![]() 的平面角,所以
的平面角,所以![]() ,所以
,所以![]() ,所以
,所以![]() .
.
(2)由(1)的(ii)知![]() 平面CFD,即
平面CFD,即![]() ,
,![]() ,所以
,所以![]() 即为二面角
即为二面角![]() 的平面角.
的平面角.
![]() .
.

练习册系列答案
相关题目